CAT 2020 Slot 2 Question Paper
For the following questions answer them individually
CAT 2020 Slot 2 - Question 61
Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
CAT 2020 Slot 2 - Question 62
In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
CAT 2020 Slot 2 - Question 63
A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other. Ram and Rahim reach their destination in one minute and four minutes, respectively. if they start at the same time, then the ratio of Ram's speed to Rahim's speed is
CAT 2020 Slot 2 - Question 64
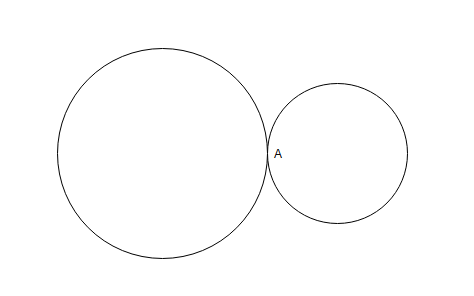
Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is
CAT 2020 Slot 2 - Question 65
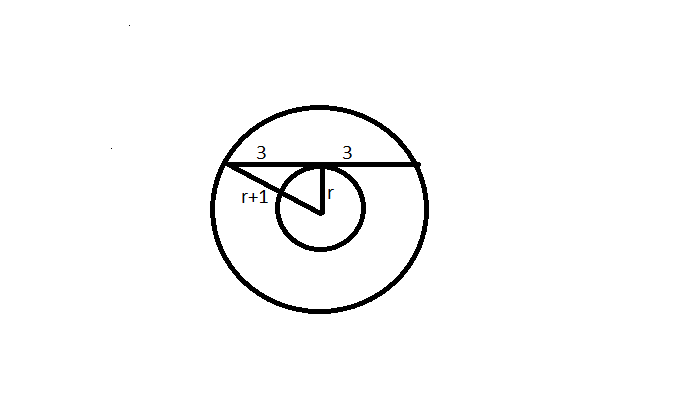
Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is
789
456
123
0.-
Clear All
CAT 2020 Slot 2 - Question 66
Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
CAT 2020 Slot 2 - Question 67
The number of integers that satisfy the equality $$(x^{2}-5x+7)^{x+1}=1$$ is
CAT 2020 Slot 2 - Question 68
The number of pairs of integers $$(x,y)$$ satisfying $$x\geq y\geq-20$$ and $$2x+5y=99$$
789
456
123
0.-
Clear All
CAT 2020 Slot 2 - Question 69
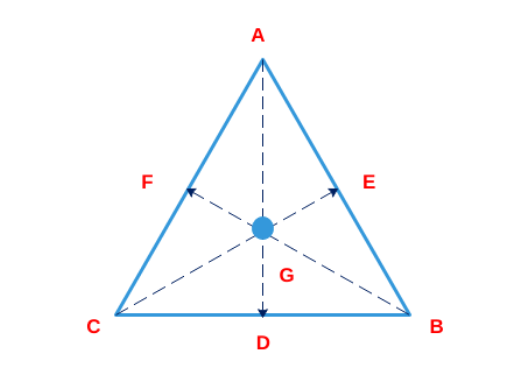
From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is
CAT 2020 Slot 2 - Question 70
Let the m-th and n-th terms of a geometric progression be $$\frac{3}{4}$$ and 12. respectively, where $$m < n$$. If the common ratio of the progression is an integer r, then the smallest possible value of $$r + n - m$$ is
Two Factor Authentication
Incase of any issue contact support@cracku.in