79+ CAT Table with Missing Values Questions PDF With Video Solutions
Practice Table with Missing values questions for CAT with detailed video solutions formulated by toppers. These type of sets frequently appear in the CAT exam. These sets require the candidate to analyze a given table and arrive at the solution. These sets require calculation skills, analyzing skills, mathematical and problem solving skills. Solve questions from CAT Previous Papers to get a fair idea of kind of sets that are being asked in the exam and also check out the free CAT mock tests and understand the types of questions that are likely to appear on the exam.
Note: No Sign-Up is required to download the PDF
Download Table with Missing Values Questions with Solutions PDF
CAT DI Tables with Missing Values Weightage Over Past 5 Years
Year | No. Of Questions |
| 2024 | 4 |
| 2023 | 5 |
2022 | 6 |
2021 | 4 |
| 2020 | 4 |
CAT 2025 Table based DI Sets questions
Anu, Bijay, Chetan, Deepak, Eshan, and Faruq are six friends. Each of them uses a mobile number from exactly one of the two mobile operators - Xitel and Yocel. During the last month, the six friends made several calls to each other. Each call was made by one of these six friends to another. The table below summarizes the number of minutes of calls that each of the six made to (outgoing minutes) and received from (incoming minutes) these friends, grouped by the operators. Some of the entries are missing.
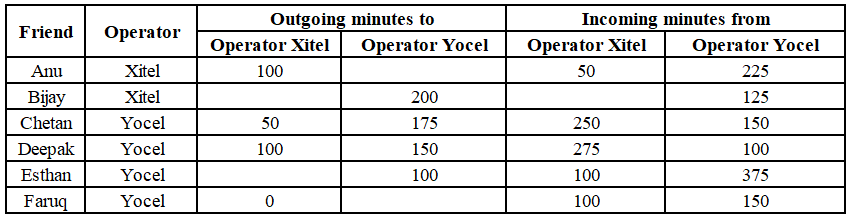
It is known that the duration of calls from Faruq to Eshan was 200 minutes. Also, there were no calls from:
i. Bijay to Eshan,
ii. Chetan to Anu and Chetan to Deepak,
iii. Deepak to Bijay and Deepak to Faruq,
iv. Eshan to Chetan and Eshan to Deepak.
Question 1
What was the duration of calls (in minutes) from Bijay to Anu?
correct answer:-50
Instruction for set 1:
Anu, Bijay, Chetan, Deepak, Eshan, and Faruq are six friends. Each of them uses a mobile number from exactly one of the two mobile operators - Xitel and Yocel. During the last month, the six friends made several calls to each other. Each call was made by one of these six friends to another. The table below summarizes the number of minutes of calls that each of the six made to (outgoing minutes) and received from (incoming minutes) these friends, grouped by the operators. Some of the entries are missing.

It is known that the duration of calls from Faruq to Eshan was 200 minutes. Also, there were no calls from:
i. Bijay to Eshan,
ii. Chetan to Anu and Chetan to Deepak,
iii. Deepak to Bijay and Deepak to Faruq,
iv. Eshan to Chetan and Eshan to Deepak.
Question 2
What was the total duration of calls (in minutes) made by Anu to friends having mobile numbers from Operator Yocel?
correct answer:-525
Instruction for set 1:
Anu, Bijay, Chetan, Deepak, Eshan, and Faruq are six friends. Each of them uses a mobile number from exactly one of the two mobile operators - Xitel and Yocel. During the last month, the six friends made several calls to each other. Each call was made by one of these six friends to another. The table below summarizes the number of minutes of calls that each of the six made to (outgoing minutes) and received from (incoming minutes) these friends, grouped by the operators. Some of the entries are missing.

It is known that the duration of calls from Faruq to Eshan was 200 minutes. Also, there were no calls from:
i. Bijay to Eshan,
ii. Chetan to Anu and Chetan to Deepak,
iii. Deepak to Bijay and Deepak to Faruq,
iv. Eshan to Chetan and Eshan to Deepak.
Question 3
What was the total duration of calls (in minutes) made by Faruq to friends having mobile numbers from Operator Yocel?
correct answer:-350
Instruction for set 1:
Anu, Bijay, Chetan, Deepak, Eshan, and Faruq are six friends. Each of them uses a mobile number from exactly one of the two mobile operators - Xitel and Yocel. During the last month, the six friends made several calls to each other. Each call was made by one of these six friends to another. The table below summarizes the number of minutes of calls that each of the six made to (outgoing minutes) and received from (incoming minutes) these friends, grouped by the operators. Some of the entries are missing.

It is known that the duration of calls from Faruq to Eshan was 200 minutes. Also, there were no calls from:
i. Bijay to Eshan,
ii. Chetan to Anu and Chetan to Deepak,
iii. Deepak to Bijay and Deepak to Faruq,
iv. Eshan to Chetan and Eshan to Deepak.
Question 4
What was the duration of calls (in minutes) from Deepak to Chetan?
correct answer:-1
CAT 2024 Table based DI Sets questions
The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100 grams of nutrients in seven food grains. The first column shows the food grain category and the second column its codename. The table has some missing values.
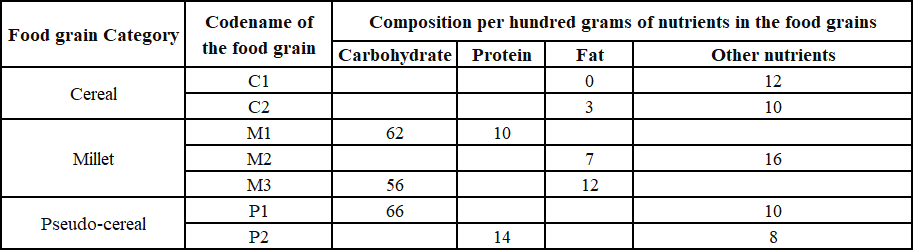
The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the food grains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the food grains are non-zero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
Question 1
How many foodgrains had a higher amount of carbohydrate per 100 grams ofnutrients than M1?
correct answer:-5
Instruction for set 1:
The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100 grams of nutrients in seven food grains. The first column shows the food grain category and the second column its codename. The table has some missing values.

The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the food grains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the food grains are non-zero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
Question 2
How many grams of protein were there in 100 grams of nutrients in M2?
correct answer:-12
Instruction for set 1:
The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100 grams of nutrients in seven food grains. The first column shows the food grain category and the second column its codename. The table has some missing values.

The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the food grains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the food grains are non-zero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
Question 3
How many grams of other nutrients were there in 100 grams of nutrients in M3?
correct answer:-24
Instruction for set 1:
The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100 grams of nutrients in seven food grains. The first column shows the food grain category and the second column its codename. The table has some missing values.

The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the food grains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the food grains are non-zero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
Question 4
What is the median of the number of grams of protein in 100 grams of nutrients among these food grains?
correct answer:-12
CAT 2023 Table based DI Sets questions
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months - January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Question 1
What was the total number of registrations in April?
correct answer:-120
Instruction for set 1:
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months - January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Question 2
What was the number of online registrations in January?
correct answer:-40
Instruction for set 1:
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months - January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Question 3
Which of the following statements can be true?
I. The number of offline registrations was the smallest in May.
II. The total number of registrations was the smallest in February.
correct answer:-4
Instruction for set 1:
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months - January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Question 4
What best can be concluded about the number of offline registrations in February?
correct answer:-4
Instruction for set 1:
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months - January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Question 5
Which pair of months definitely had the same total number of registrations?
I. January and April
II. February and May
correct answer:-1
Instruction for set 2:
Odsville has five firms - Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores. The table below provides partial information about the five firms.

Question 6
For which firm(s) can the amounts raised by them be concluded with certainty in each year?
correct answer:-2
Instruction for set 2:
Odsville has five firms - Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores. The table below provides partial information about the five firms.

Question 7
What best can be concluded about the total amount of money raised in 2015?
correct answer:-3
Instruction for set 2:
Odsville has five firms - Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores. The table below provides partial information about the five firms.

Question 8
What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
correct answer:-17
Instruction for set 2:
Odsville has five firms - Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores. The table below provides partial information about the five firms.

Question 9
If Elavalaki raised Rs. 3 crores in 2013, then what is the smallest possible total amount of money (in Rs. crores) that could have been raised by all the companies in 2012?
correct answer:-3
Instruction for set 2:
Odsville has five firms - Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores. The table below provides partial information about the five firms.

Question 10
If the total amount of money raised in 2014 is Rs. 12 crores, then which of the following is not possible?
correct answer:-1
Instruction for set 3:
There are only three female students - Amala, Koli and Rini - and only three male students - Biman, Mathew and Shyamal - in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical - 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala’s score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
Question 11
What was Rini’s score in the project?
correct answer:-60
Instruction for set 3:
There are only three female students - Amala, Koli and Rini - and only three male students - Biman, Mathew and Shyamal - in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical - 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala’s score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
Question 12
What was the weight of the test component?
correct answer:-1


