Please enter the following details
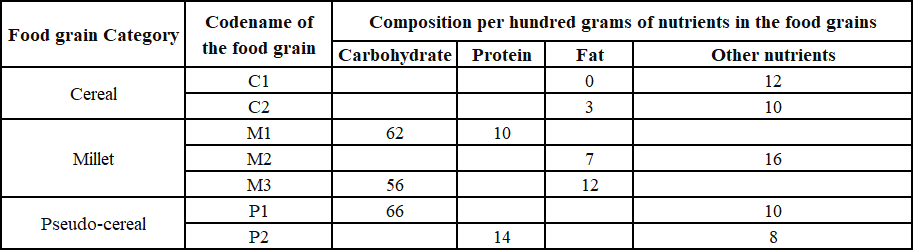
The table given below shows the amount, in grams, of carbohydrate, protein, fat and all other nutrients, per 100 grams of nutrients in seven food grains. The first column shows the food grain category and the second column its codename. The table has some missing values.
The following additional facts are known.
1. Both the pseudo-cereals had higher amounts of carbohydrate as well as higher amounts of protein than any millet.
2. Both the cereals had higher amounts of carbohydrate than any pseudo-cereal.
3. All the missing values of carbohydrate amounts (in grams) for all the food grains are non-zero multiples of 5.
4. All the missing values of protein, fat and other nutrients amounts (in grams) for all the food grains are non-zero multiples of 4.
5. P1 contained double the amount of protein that M3 contains.
What is the median of the number of grams of protein in 100 grams of nutrientsamong these food grains?
Correct Answer: 12
The set's starting point is that the sum of each row must be 100
Clue 3 tells us that all the missing elements in the Carbs column are multiple of 5. Similarly, clue 4 tells us that the missing elements of the other three columns are multiples of 4.
Note that we look at clue 1, which says that the carbs in C1 and C2 must be more than any carbs in any pseudo cereal.
We have the reference point of P1 at 66
Trying to fill in for C1:
The possible values are 75, 80, 85, 90, 95
Since 12 grams is of other nutrients, we can eliminate 90 and 95.
If we take 85, 85+12 = 97, which would leave 3 grams of protein, but from clue 4, we know this has to be a multiple of 4.
Taking 75, 75+12 = 87 would leave 13 grams of protein, which, too, is eliminated.
Leaving only 80 grams of carb in C1 and 8 grams of protein.
Similar logic is to be applied for C2; we have 13 grams already present, so the values of 90 and 95 are eliminated.
Taking 85 carbs would give 2 grams of protein, which can be eliminated.
80 and 70 would also not work for the same reason.
Leavin has only 75 grams of carbs, leaving 12 grams of protein.
Using clues 1 and 2 together, we can determine that the carbs in P2 must be less than 75 but at least greater than 62.
The only possible values are 65 and 70
Putting 65 grams of carbs in P2 gives us 100-65-14-8 = 13 grams of protein, which is invalid.
Putting 70 grams of carbs in P2 gives 100-70-14-8 = 8 grams of protein.
Clue 1 gives us that the protein in M2 should be less than that present in either of the pseudo-cereals, which we right now have a baseline of 14.
So the protein in M2 (and M3) can be 12, 8, 4, 0
The protein and carbs in M2 should add up to 100-7-16 = 77
This is only possible if the protein count is 12, giving carbs as 65
The protein in M3 can be 0, 4, 8 or 12
We are given in clue five that the protein in P1 is double that in M3.
The protein in P1 thus can be 0, 8, 16 or 24
Since this P1 protein also has to be more than M1 and M2 protein, it can not be 0 or 8
Leaving only 16 or 24 as the valid values.
The protein and fats in P1 must add up to 100-66-10 = 24
If P1 had 24 grams of protein, then it would have 0 grams of fat, but in clue 4, we are given that all missing fats are non-zero multiples of 4
Hence, the only possible protein value in P1 is 16, with 8 grams of fats. Giving 8 grams of protein in M3 and 24 grams of others in M3.
The proteins in the foodgrains, when arranged in ascending order, are: 8, 8, 10, 12, 12,14, 16
Giving the median as 12.
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
