Sign in
Please select an account to continue using cracku.in
↓ →
CAT WhatsApp Group
Consider two sets $$A = \left\{2, 3, 5, 7, 11, 13 \right\}$$ and $$B = \left\{1, 8, 27 \right\}$$. Let f be a function from A to B such that for every element in B, there is at least one element a in A such that $$f(a) = b$$. Then, the total number of such functions f is
Set A={2,3,5,7,11,13} so |A|=6
Set B={1, 8, 27} so |B|=3
Without any restrictions, each element in A can map to any of the 3 elements in B. Thus, the total number of functions is: $$3^6=729$$
Excluding Functions That Miss One Element in B: If a function does not map to an element in B, there are 2 elements in B left for mapping. The total number of such functions (for each specific element not mapped) is: $$2^6=64$$
Since there are 3 elements in B, the total number of such functions is:3x64=192
Adding Back Functions That Miss Two Elements in B:
If a function misses two elements in B, there is only 1 element left for mapping. The total number of such functions is: 1^6=1.
Since there are $$^3C_2$$ ways to choose which two elements are missed, the total number of such functions is: 3
Using the inclusion-exclusion principle, the number of functions where all elements of B are mapped by at least one element of A is:
729-192+3=540.
Let $$x, y,$$ and $$z$$ be real numbers satisfying
$$4(x^{2}+y^{2}+z^{2})=a,$$
$$4(x-y-z)=3+a$$
The a equals
Loading solution...
lf the equations $$x^{2}+mx+9=0, x^{2}+nx+17=0$$ and $$x^{2}+(m+n)x+35=0$$ have a common negative root, then the value of $$(2m+3n)$$ is
Loading solution...
Suppose $$x_{1},x_{2},x_{3},...,x_{100}$$ are in arithmetic progression such that $$x_{5}=-4$$ and $$2x_{6}+2x_{9}=x_{11}+x_{13}$$, Then,$$x_{100}$$ equals
Loading solution...
Renu would take 15 days working 4 hours per day to complete a certain task whereas Seema would take 8 days working 5 hours per day to complete the same task. They decide to work together to complete this task. Seema agrees to work for double the number of hours per day as Renu, while Renu agrees to work for double the number of days as Seema. If Renu works 2 hours per day, then the number of days Seema will work, is
Loading solution...
When $$10^{100}$$is divided by 7, the remainder is
Loading solution...
The sum of all real values of k for which $$\left(\cfrac{1}{8}\right)^{k}\times \left(\cfrac{1}{32768}\right)^{\cfrac{1}{3}}=\cfrac{1}{8}\times \left(\cfrac{1}{32768}\right)^{\cfrac{1}{k}}$$, is
Loading solution...
For any natural number $$n$$ let $$a_{n}$$ be the largest integer not exceeding $$\sqrt{n}$$. Then the value of $$a_{1}+a_{2}+.....+a_{50}$$ is
Loading solution...
In September, the incomes of Kamal, Amal and Vimal are in the ratio 8 ∶ 6 ∶ 5. They rent a house together, and Kamal pays 15%, Amal pays 12% and Vimal pays 18% of their respective incomes to cover the total house rent in that month. In October, the house rent remains unchanged while their incomes increase by 10%, 12% and 15%, respectively. In October, the percentage of their total income that will be paid as house rent, is nearest to
Loading solution...
The sum of all four-digit numbers that can be formed with the distinct non-zero digits a, b, c, and d, with each digit appearing exactly once in every number, is 153310 + n, where n is a single digit natural number. Then, the value of (a + b + c + d + n) is
Loading solution...
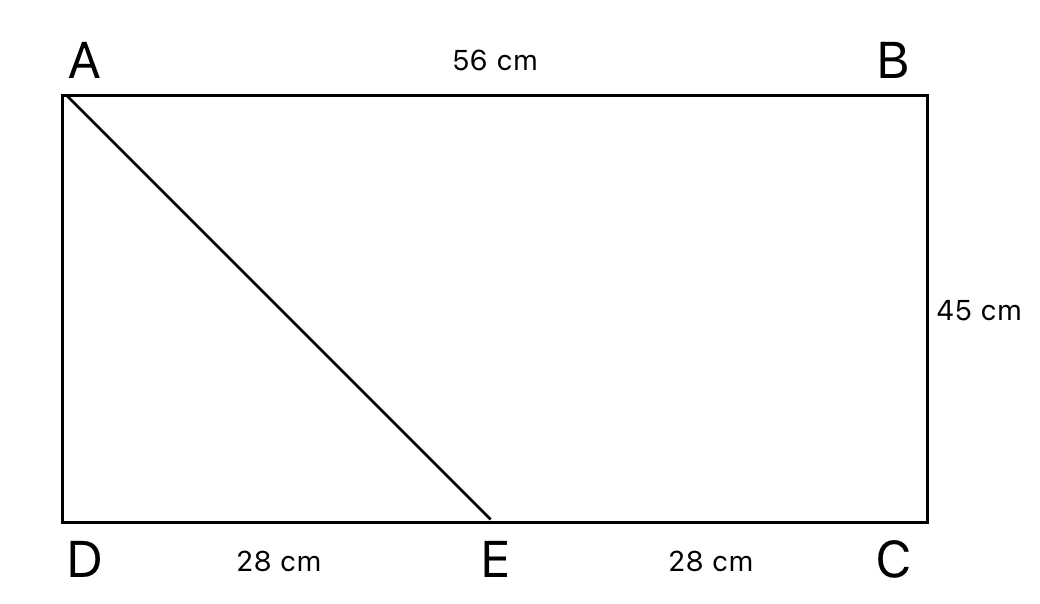
ABCD is a rectangle with sides AB = 56 cm and BC = 45 cm, and E is the midpoint of side CD. Then, the length, in cm, of radius of incircle of $$\triangle ADE$$ is
Loading solution...
In the XY-plane, the area, in sq. units, of the region defined by the inequalities
$$y \geq x + 4$$ and $$-4 \leq x^2 + y^2 + 4(x - y) \leq 0$$ is
Loading solution...
If x is a positive real number such that $$4 \log_{10} x + 4 \log_{100} x + 8 \log_{1000} x = 13$$, then the greatest integer not exceeding x, is
Loading solution...
The selling price of a product is fixed to ensure 40% profit. If the product had cost 40% less and had been sold for 5 rupees less, then the resulting profit would have been 50%. The original selling price, in rupees, of the product is
Loading solution...
A glass is filled with milk. Two-thirds of its content is poured out and replaced with water. If this process of pouring out two-thirds the content and replacing with water is repeated three more times, then the final ratio of milk to water in the glass, is
Loading solution...
A fruit seller has a total of 187 fruits consisting of apples, mangoes and oranges. The number of apples and mangoes are in the ratio 5 : 2. After she sells 75 apples, 26 mangoes and half of the oranges, the ratio of number of unsold apples to number of unsold oranges becomes 3 : 2. The total number of unsold fruits is
Loading solution...
Two places A and B are 45 kms apart and connected by a straight road. Anil goes from A to B while Sunil goes from B to A. Starting at the same time, they cross each other in exactly 1 hour 30 minutes. If Anil reaches B exactly 1 hour 15 minutes after Sunil reaches A, the speed of Anil, in km per hour, is
Loading solution...
There are four numbers such that average of first two numbers is 1 more than the first number, average of first three numbers is 2 more than average of first two numbers, and average of first four numbers is 3 more than average of first three numbers. Then, the difference between the largest and the smallest numbers, is
Loading solution...
An amount of Rs 10000 is deposited in bank A for a certain number of years at a simple interest of 5% per annum. On maturity, the total amount received is deposited in bank B for another 5 years at a simple interest of 6% per annum. If the interests received from bank A and bank B are in the ratio 10 : 13, then the investment period, in years, in bank A is
Loading solution...
A shop wants to sell a certain quantity (in kg) of grains. It sells half the quantity and an additional 3 kg of these grains to the first customer. Then, it sells half of the remaining quantity and an additional 3 kg of these grains to the second customer. Finally, when the shop sells half of the remaining quantity and an additional 3 kg of these grains to the third customer, there are no grains left. The initial quantity, in kg, of grains is
Loading solution...
If $$(a + b \sqrt{n})$$ is the positive square root of $$(29 - 12\sqrt{5})$$, where a and b are integers, and n is a natural number, then the maximum possible value of $$(a + b + n)$$ is
Loading solution...
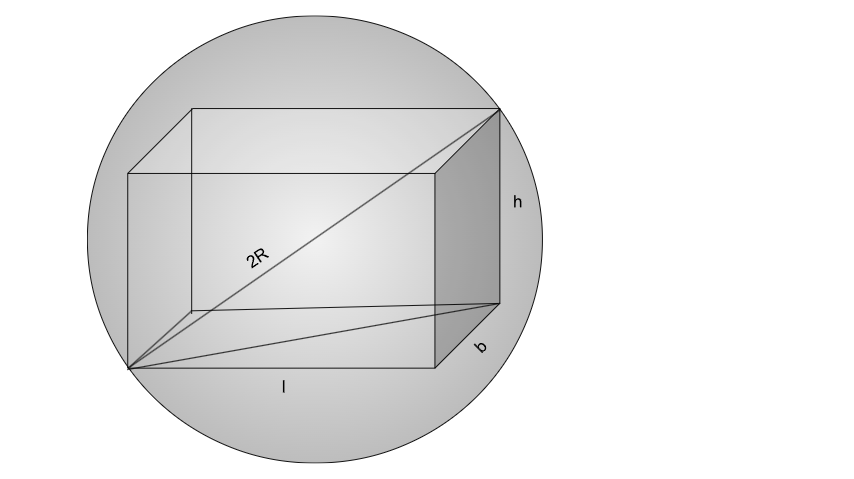
The surface area of a closed rectangular box, which is inscribed in a sphere, is 846 sq cm, and the sum of the lengths of all its edges is 144 cm. The volume, in cubic cm, of the sphere is
Loading solution...
Start your IIM journey with the right preparation and crack CAT 2026.
Educational materials for CAT preparation
91- 6303239042
Share
