Sign in
Please select an account to continue using cracku.in
↓ →
The sum of all real values of k for which $$\left(\cfrac{1}{8}\right)^{k}\times \left(\cfrac{1}{32768}\right)^{\cfrac{1}{3}}=\cfrac{1}{8}\times \left(\cfrac{1}{32768}\right)^{\cfrac{1}{k}}$$, is
To solve this question, we need to immediately recognise the fact that, $$32768=8^5$$
Substituting this in the above given equation,
$$\left(\dfrac{1}{8}\right)^k\times\ \left(\dfrac{1}{8}\right)^{5\times\ \dfrac{1}{3}}=\left(\dfrac{1}{8}\right)\times\ \left(\dfrac{1}{8}\right)^{5\times\ \dfrac{1}{k}}$$
Since the bases are equal, we can equate the powers on either side of the equation,
$$k+\frac{5}{3}=1+\frac{5}{k}$$
$$\frac{\left(3k+5\right)}{3}=\frac{\left(k+5\right)}{k}$$
$$3k^2+5k=3k+15$$
$$3k^2+2k-15=0$$
Here in the given quadratic equation, the Discriminant is greater than 0, $$2^2-\left(4\right)\left(3\right)\left(-15\right)>0$$
That means both the roots are real, hence we can simply take the sum of the roots of the quadratic equation in k,
Which in a standard quadratic equation of the form $$ax^2+bx+c$$ is $$-\frac{b}{a}$$
Here, the sum of the real values of k is $$-\frac{2}{3}$$
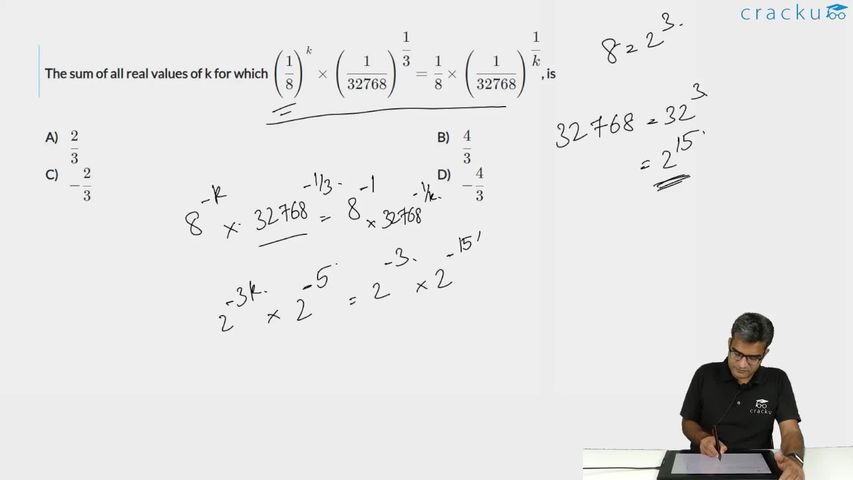
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation