Join WhatsApp Icon CAT WhatsApp Group
Question 57

ABCD is a rectangle with sides AB = 56 cm and BC = 45 cm, and E is the midpoint of side CD. Then, the length, in cm, of radius of incircle of $$\triangle ADE$$ is


Correct Answer: 10

Solution

Share

Drawing the figure described in the question, we get the following representation, 

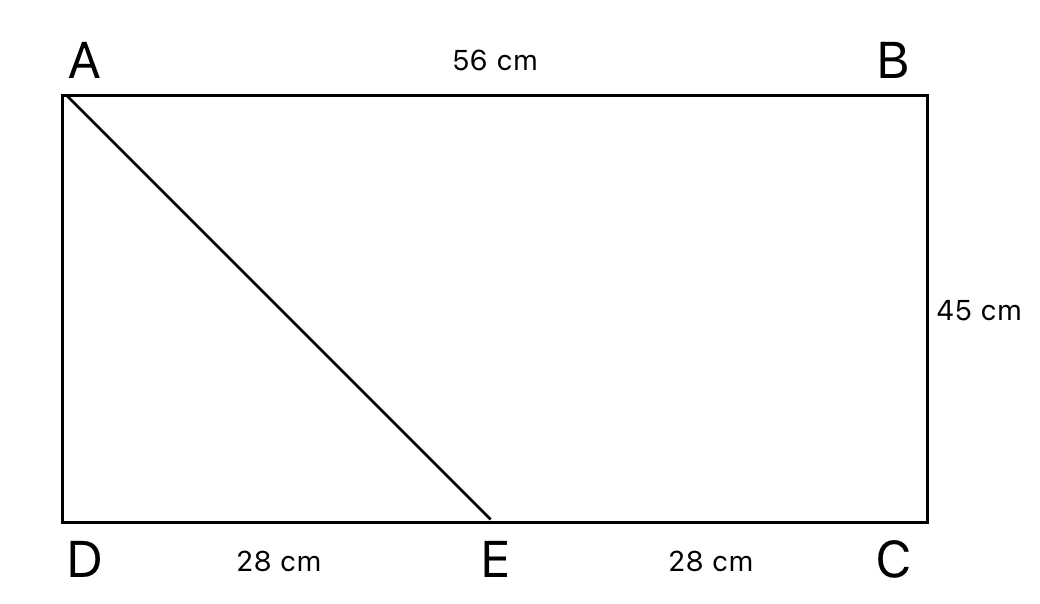
Screenshot 2024-12-04 at 10

Since E is the midpoint of CD, the length of each half will be 28cm. 

We need to find the incircle of the triangle ADE, which is a right angled triangle, we can do that with the formula, 
$$\dfrac{\left(a+b-h\right)}{2}$$

$$h^2=28^2+45^2$$
$$h^2=784+2025=2809$$
$$h=53$$

$$r=\dfrac{\left(28+45-53\right)}{2}=10$$

Get AI Help

Video Solution

video
View More Questions From Geometry

Create a FREE account and get:

  • All Quant CAT complete Formulas and shortcuts PDF
  • 41+ CAT previous year papers with video solutions PDF
  • 5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Time Speed Distance QuestionsCAT Arithmetic QuestionsCAT Remainders QuestionsCAT Mensuration QuestionsCAT Quadratic Equations Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Data change over a period QuestionsCAT Data Interpretation Basics QuestionsCAT Special Charts QuestionsCAT Scheduling QuestionsCAT Selection With Condition Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Critical Reasoning QuestionsCAT Grammar and Sentence Correction QuestionsCAT Para Summary QuestionsCAT Reading Comprehension QuestionsCAT Vocabulary Questions

Free CAT Quant Questions

CAT GeometryCAT Number SystemsCAT Probability, CombinatoricsCAT Averages Mixtures AlligationsCAT Averages, Ratio and ProportionCAT LogarithmsCAT ArithmeticCAT AveragesCAT Number SeriesCAT Time And WorkCAT Linear EquationsCAT InequalitiesCAT Functions, Graphs and StatisticsCAT RemaindersCAT Simple Interest Compound InterestCAT Profit and LossCAT MiscellaneousCAT Time, Speed and DistanceCAT Venn DiagramsCAT AlgebraCAT Quadratic EquationsCAT Logarithms, Surds and IndicesCAT MensurationCAT Profit And LossCAT Time Speed DistanceCAT Progressions and SeriesCAT Data SufficiencyCAT PercentagesCAT Coordinate Geometry

Related Formulas With Tests

Quadrilateral - Areas and other formulas Triangles - Centroid, circum radius and inradius

Book Free CAT Mentorship

Get personalized CAT strategy from a 99%iler

500+ students mentored
CAT mentor

Join CAT 2026 course by 5-Time CAT 100%iler

Start your IIM journey with the right preparation and crack CAT 2026.

Enroll Now
Ask AI