Given that, The surface area of a closed rectangular box, which is inscribed in a sphere, is 846 sq cm
So, $$2(lb+bh+hl)=846$$. 

And $$4(l+b+h)=144$$
$$(l+b+h)=36$$
$$\left(l+b+h\right)^2=l^2+b^2+h^2+2\left(lb+bh+hl\right)$$
$$1296=\left(l^2+b^2+h^2\right)+846$$
$$450=l^2+b^2+h^2$$

We are told that this cuboid is inscribed in a sphere, the body diagonal of the cuboid equals the diameter of the sphere, this can be visualised as:

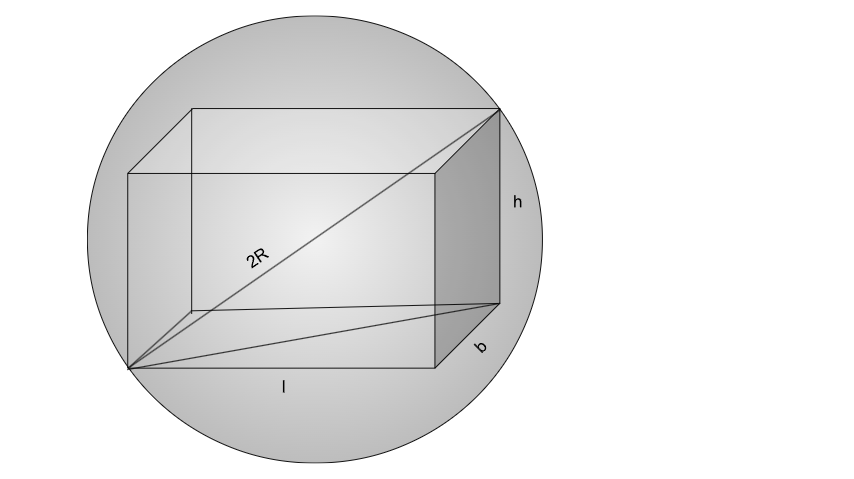
This is nothing but, $$\sqrt{l^2+b^2+h^2}=2R$$
$$l^2+b^2+h^2=4R^2$$
$$450=4R^2$$
$$R^2=\frac{225}{2}$$
$$R=\frac{15}{\sqrt{2}}$$

Volume of sphere will be $$\dfrac{4}{3}\times\ \pi\ \times\ \left(\dfrac{15}{\sqrt{2}}\right)^3$$

$$\dfrac{4}{3}\pi\ \left(\dfrac{3375}{2\sqrt{\ 2}}\right)$$

$$\pi\ \times\ 1125\sqrt{\ 2}$$