CAT 2017 Slot 1 Quant Question Paper
For the following questions answer them individually
CAT 2017 Slot 1 Quant - Question 67
Arun's present age in years is 40% of Barun's. In another few years, Arun's age will be half of Barun's. By what percentage will Barun's age increase during this period?
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 68
A person can complete a job in 120 days. He works alone on Day 1. On Day 2, he is joined by another person who also can complete the job in exactly 120 days. On Day 3, they are joined by another person of equal efficiency. Like this, everyday a new person with the same efficiency joins the work. How many days are required to complete the job?
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 69
An elevator has a weight limit of 630 kg. It is carrying a group of people of whom the heaviest weighs 57 kg and the lightest weighs 53 kg. What is the maximum possible number of people in the group?
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 70
A man leaves his home and walks at a speed of 12 km per hour, reaching the railway station 10 minutes after the train had departed. If instead he had walked at a speed of 15 km per hour, he would have reached the station 10 minutes before the train's departure. The distance (in km) from his home to the railway station is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 71
Ravi invests 50% of his monthly savings in fixed deposits. Thirty percent of the rest of his savings is invested in stocks and the rest goes into Ravi's savings bank account. If the total amount deposited by him in the bank (for savings account and fixed deposits) is Rs 59500, then Ravi's total monthly savings (in Rs) is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 72
If a seller gives a discount of 15% on retail price, she still makes a profit of 2%. Which of the following ensures that she makes a profit of 20%?
CAT 2017 Slot 1 Quant - Question 73
A man travels by a motor boat down a river to his office and back. With the speed of the river unchanged, if he doubles the speed of his motor boat, then his total travel time gets reduced by 75%. The ratio of the original speed of the motor boat to the speed of the river is
CAT 2017 Slot 1 Quant - Question 74
Suppose, C1, C2, C3, C4, and C5 are five companies. The profits made by Cl, C2, and C3 are in the ratio 9 : 10 : 8 while the profits made by C2, C4, and C5 are in the ratio 18 : 19 : 20. If C5 has made a profit of Rs 19 crore more than C1, then the total profit (in Rs) made by all five companies is
CAT 2017 Slot 1 Quant - Question 75
The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
CAT 2017 Slot 1 Quant - Question 76
A stall sells popcorn and chips in packets of three sizes: large, super, and jumbo. The numbers of large, super, and jumbo packets in its stock are in the ratio 7 : 17 : 16 for popcorn and 6 : 15 : 14 for chips. If the total number of popcorn packets in its stock is the same as that of chips packets, then the numbers of jumbo popcorn packets and jumbo chips packets are in the ratio
CAT 2017 Slot 1 Quant - Question 77
In a market, the price of medium quality mangoes is half that of good mangoes. A shopkeeper buys 80 kg good mangoes and 40 kg medium quality mangoes from the market and then sells all these at a common price which is 10% less than the price at which he bought the good ones. His overall profit is
CAT 2017 Slot 1 Quant - Question 78
If Fatima sells 60 identical toys at a 40% discount on the printed price, then she makes 20% profit. Ten of these toys are destroyed in fire. While selling the rest, how much discount should be given on the printed price so that she can make the same amount of profit?
CAT 2017 Slot 1 Quant - Question 79
If a and b are integers of opposite signs such that $$(a + 3)^{2} : b^{2} = 9 : 1$$ and $$(a -1)^{2}:(b - 1)^{2} = 4:1$$, then the ratio $$a^{2} : b^{2}$$ is
CAT 2017 Slot 1 Quant - Question 80
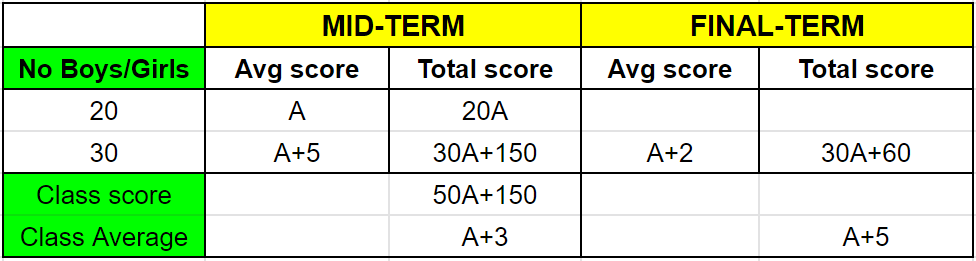
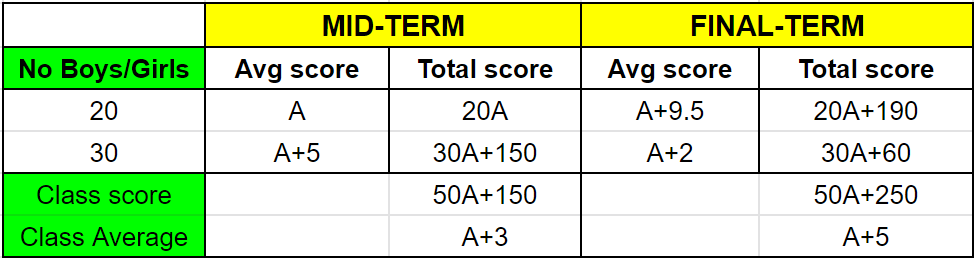
A class consists of 20 boys and 30 girls. In the mid-semester examination, the average score of the girls was 5 higher than that of the boys. In the final exam, however, the average score of the girls dropped by 3 while the average score of the entire class increased by 2. The increase in the average score of the boys is
CAT 2017 Slot 1 Quant - Question 81
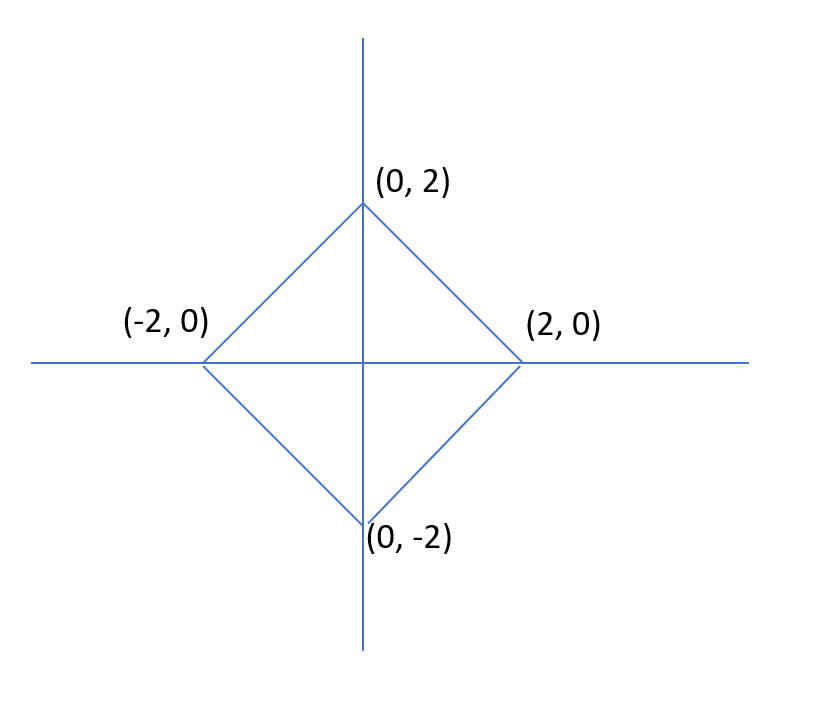
The area of the closed region bounded by the equation
I x I + I y I = 2 in the two-dimensional plane is
CAT 2017 Slot 1 Quant - Question 82
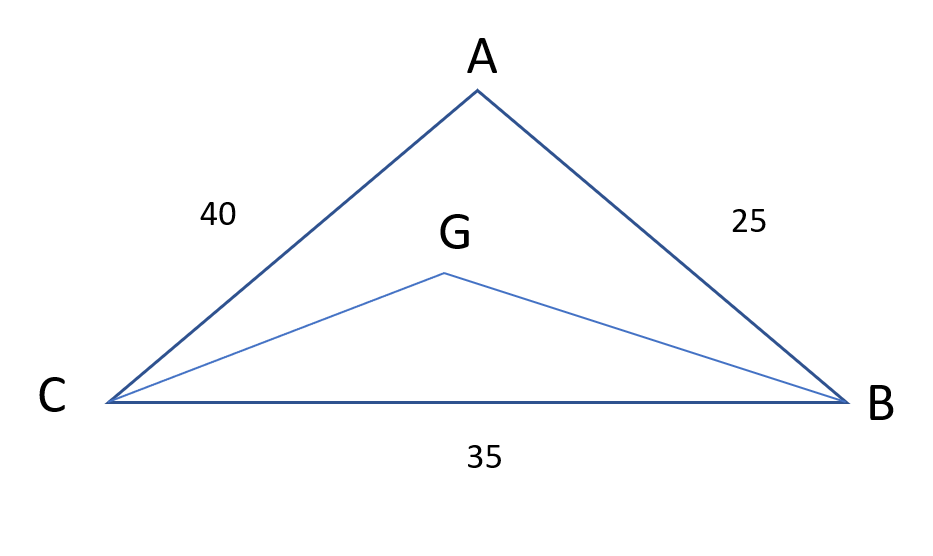
From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
CAT 2017 Slot 1 Quant - Question 83
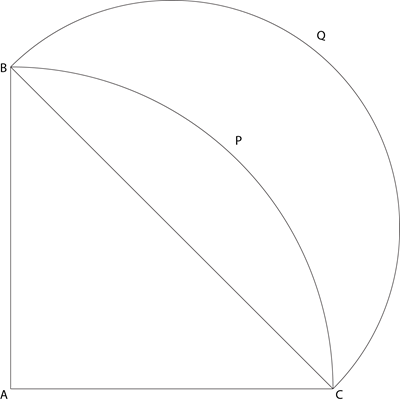
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
CAT 2017 Slot 1 Quant - Question 84
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to
CAT 2017 Slot 1 Quant - Question 85
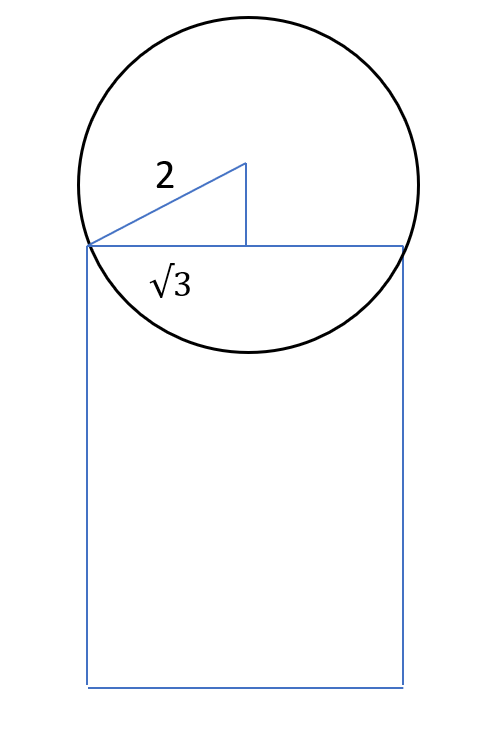
A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is $$9\pi$$ cubic centimeters. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 86
Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 87
Suppose, $$\log_3 x = \log_{12} y = a$$, where $$x, y$$ are positive numbers. If $$G$$ is the geometric mean of x and y, and $$\log_6 G$$ is equal to
CAT 2017 Slot 1 Quant - Question 89
The value of $$\log_{0.008}\sqrt{5}+\log_{\sqrt{3}}81-7$$ is equal to
CAT 2017 Slot 1 Quant - Question 91
The number of solutions $$(x, y, z)$$ to the equation $$x - y - z = 25$$, where x, y, and z are positive integers such that $$x\leq40,y\leq12$$, and $$z\leq12$$ is
CAT 2017 Slot 1 Quant - Question 92
For how many integers n, will the inequality $$(n - 5) (n - 10) - 3(n - 2)\leq0$$ be satisfied?
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 93
If $$f_{1}(x)=x^{2}+11x+n$$ and $$f_{2}(x)=x$$, then the largest positive integer n for which the equation $$f_{1}(x)=f_{2}(x)$$ has two distinct real roots is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 94
If $$a, b, c,$$ and $$d$$ are integers such that $$a+b+c+d=30$$ then the minimum possible value of $$(a - b)^{2} + (a - c)^{2} + (a - d)^{2}$$ is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 95
Let AB, CD, EF, GH, and JK be five diameters of a circle with center at 0. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K, and O so as to form a triangle?
789
456
123
0.-
Clear All
CAT 2017 Slot 1 Quant - Question 96
The shortest distance of the point $$(\frac{1}{2},1)$$ from the curve y = I x -1I + I x + 1I is
CAT 2017 Slot 1 Quant - Question 97
If the square of the 7th term of an arithmetic progression with positive common difference equals the product of the 3rd and 17th terms, then the ratio of the first term to the common difference is
CAT 2017 Slot 1 Quant - Question 98
In how many ways can 7 identical erasers be distributed among 4 kids in such a way that each kid gets at least one eraser but nobody gets more than 3 erasers?
CAT 2017 Slot 1 Quant - Question 99
$$f(x) = \frac{5x+2}{3x-5}$$ and $$g(x) = x^2 - 2x - 1$$, then the value of $$g(f(f(3)))$$ is
CAT 2017 Slot 1 Quant - Question 100
Let $$a_1$$, $$a_2$$,............., $$a_{3n}$$ be an arithmetic progression with $$a_1$$ = 3 and $$a_{2}$$ = 7. If $$a_1$$+ $$a_{2}$$ +...+ $$a_{3n}$$= 1830, then what is the smallest positive integer m such that m($$a_1$$+ $$a_{2}$$ +...+ $$a_n$$) > 1830?
Two Factor Authentication
Incase of any issue contact support@cracku.in