Question 85

A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is $$9\pi$$ cubic centimeters. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is

Correct Answer: 6

Solution

The volume of a cylinder is $$\pi * r^2 * 3 = 9 \pi$$

r = $$\sqrt{3}$$ cm.

Radius of the ball is 2 cm. Hence, the ball will lie on top of the cylinder.

Lets draw the figure.

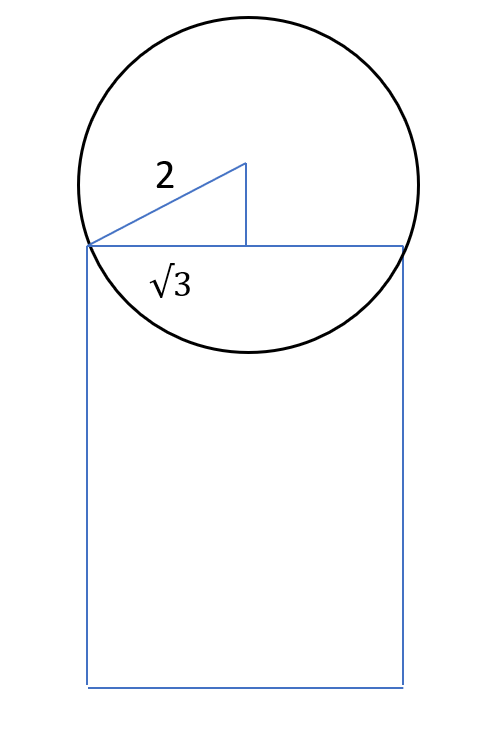
Based on the Pythagoras theorem, the other leg will be 1 cm.

Thus, the height will be 3 + 1 + 2 = 6 cm

Click on the Email ☝️ to Watch the Video Solution

Create a FREE account and get:

CAT Quant Questions | CAT Quantitative Ability