Sign in
Please select an account to continue using cracku.in
↓ →
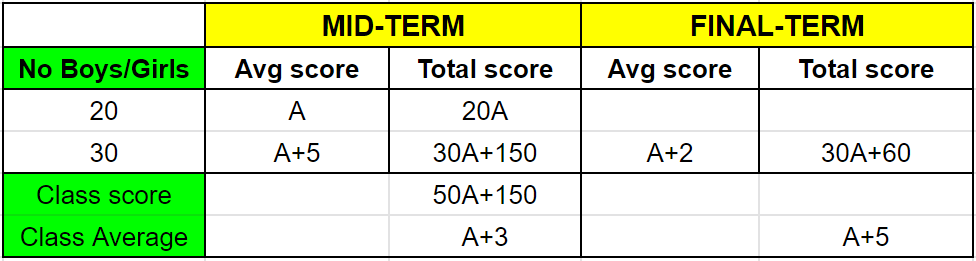
A class consists of 20 boys and 30 girls. In the mid-semester examination, the average score of the girls was 5 higher than that of the boys. In the final exam, however, the average score of the girls dropped by 3 while the average score of the entire class increased by 2. The increase in the average score of the boys is
Let, the average score of boys in the mid semester exam is A.
Therefore, the average score of girls in the mid semester exam be A+5.
Hence, the total marks scored by the class is $$20\times (A) + 30\times (A+5) = 50\times A + 150$$
The average score of the entire class is $$\dfrac{(50\times A + 150)}{50} = A + 3$$
wkt, class average increased by 2, class average in final term $$= (A+3) + 2 = A + 5$$
Given, that score of girls dropped by 3, i.e $$(A+5)-3 = A+2$$
Total score of girls in final term $$= 30\times(A+2) = 30A + 60$$
Total class score in final term $$= (A + 5)\times50 = 50A + 250$$
the total marks scored by the boys is $$(50A + 250) - (30A - 60) = 20A + 190$$
Hence, the average of the boys in the final exam is $$\dfrac{(20G + 190)}{20} = A + 9.5$$
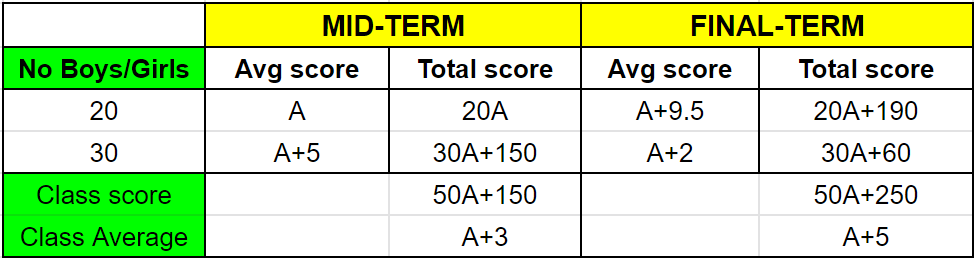
Hence, the increase in the average marks of the boys is $$(A+9.5) - A = 9.5$$

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation