Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is

The image of the figure is as shown. 

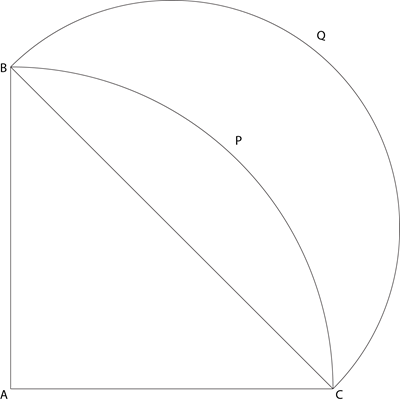
AB = AC = 6cm. Thus, BC = $$\sqrt{6^2 + 6^2}$$ = 6√2 cm

The required area = Area of semi-circle BQC - Area of quadrant BPC + Area of triangle ABC

Area of semicircle BQC

Diameter BC = 6√2cm

Radius = 6√2/2 = 3√2 cm

Area = $$\pi r^2 $$/2 = $$ \pi$$ * $$(3 \sqrt{2})^2 $$/2 = 9$$\pi$$

Area of quadrant BPC

Area = $$\pi r^2$$/4 = $$\pi*(6)^2$$/4 = 9$$\pi$$

Area of triangle ABC

Area = 1/2 * 6 * 6 = 18

The required area = Area of semi-circle BQC - Area of quadrant BPC + Area of triangle ABC

= 9$$\pi$$ - 9$$\pi$$ + 18 = 18