Top 121+ CAT DILR Arrangement Questions PDF With Video Solutions
Practice Arrangement questions for CAT with detailed video solutions. Arrangement questions were consistent in the CAT exam across the years. Every year atleast 5 to 6 questions used to commonly appear in the exam. These questions essentially requires the student to find a single solution where he could satisfy all the mentioned conditions. To get a more better understanding practice questions from CAT Previous Papers which will give you a better understanding of the kind and type of questions being asked in the exam across years.
Note: No Sign-Up is required to download the PDF
CAT DILR Arrangement Sets Weightage Over Past 6 Years
Year |
No. Of Questions |
| 2025 | 8 |
| 2024 | 9 |
| 2023 | 4 |
2022 | 0 |
2021 | 0 |
| 2020 | 8 |
CAT 2025 Arrangement questions
A round table has seven chairs around it. The chairs are numbered 1 through 7 in a clockwise direction. Four friends, Aslam, Bashir, Chhavi, and Davies, sit on four of the chairs. In the starting position, Aslam and Chhavi are sitting next to each other, while for Bashir as well as Davies, there are empty chairs on either side of the chairs that are sitting on.
The friends take turns moving either clockwise or counterclockwise from their chair. The friend who has to move in a turn occupies the first empty chair in whichever direction (s)he chooses to move. Aslam moves first (Turn 1), followed by Bashir, Chhavi, and Davies (Turns 2, 3, and 4, respectively). Then Aslam moves again followed by Bashir, and Chhavi (Turns 5, 6, and 7, respectively).
The following information is known
1. The four friends occupy adjacent chairs only at the end of Turn 2 and Turn 6.
2. Davies occupies Chair 2 after Turn 1 and Chair 4 after Turn 5, and Chhavi occupies Chair 7 after Turn 2.
Question 1
What is the number of the chair initially occupied by Bashir?
correct answer:-4
Instruction for set 1:
A round table has seven chairs around it. The chairs are numbered 1 through 7 in a clockwise direction. Four friends, Aslam, Bashir, Chhavi, and Davies, sit on four of the chairs. In the starting position, Aslam and Chhavi are sitting next to each other, while for Bashir as well as Davies, there are empty chairs on either side of the chairs that are sitting on.
The friends take turns moving either clockwise or counterclockwise from their chair. The friend who has to move in a turn occupies the first empty chair in whichever direction (s)he chooses to move. Aslam moves first (Turn 1), followed by Bashir, Chhavi, and Davies (Turns 2, 3, and 4, respectively). Then Aslam moves again followed by Bashir, and Chhavi (Turns 5, 6, and 7, respectively).
The following information is known
1. The four friends occupy adjacent chairs only at the end of Turn 2 and Turn 6.
2. Davies occupies Chair 2 after Turn 1 and Chair 4 after Turn 5, and Chhavi occupies Chair 7 after Turn 2.
Question 2
Who sits on the chair numbered 4 at the end of Turn 3?
correct answer:-4
Instruction for set 1:
A round table has seven chairs around it. The chairs are numbered 1 through 7 in a clockwise direction. Four friends, Aslam, Bashir, Chhavi, and Davies, sit on four of the chairs. In the starting position, Aslam and Chhavi are sitting next to each other, while for Bashir as well as Davies, there are empty chairs on either side of the chairs that are sitting on.
The friends take turns moving either clockwise or counterclockwise from their chair. The friend who has to move in a turn occupies the first empty chair in whichever direction (s)he chooses to move. Aslam moves first (Turn 1), followed by Bashir, Chhavi, and Davies (Turns 2, 3, and 4, respectively). Then Aslam moves again followed by Bashir, and Chhavi (Turns 5, 6, and 7, respectively).
The following information is known
1. The four friends occupy adjacent chairs only at the end of Turn 2 and Turn 6.
2. Davies occupies Chair 2 after Turn 1 and Chair 4 after Turn 5, and Chhavi occupies Chair 7 after Turn 2.
Question 3
Which of the chairs are occupied at the end of Turn 6?
correct answer:-1
Instruction for set 1:
A round table has seven chairs around it. The chairs are numbered 1 through 7 in a clockwise direction. Four friends, Aslam, Bashir, Chhavi, and Davies, sit on four of the chairs. In the starting position, Aslam and Chhavi are sitting next to each other, while for Bashir as well as Davies, there are empty chairs on either side of the chairs that are sitting on.
The friends take turns moving either clockwise or counterclockwise from their chair. The friend who has to move in a turn occupies the first empty chair in whichever direction (s)he chooses to move. Aslam moves first (Turn 1), followed by Bashir, Chhavi, and Davies (Turns 2, 3, and 4, respectively). Then Aslam moves again followed by Bashir, and Chhavi (Turns 5, 6, and 7, respectively).
The following information is known
1. The four friends occupy adjacent chairs only at the end of Turn 2 and Turn 6.
2. Davies occupies Chair 2 after Turn 1 and Chair 4 after Turn 5, and Chhavi occupies Chair 7 after Turn 2.
Question 4
Which of the following BEST describes the friends sitting on chairs adjacent to the one occupied by Bashir at the end of Turn 7?
correct answer:-2
Instruction for set 2:
Seven children, Aarav, Bina, Chirag, Diya, Eshan, Farhan, and Gaurav, are sitting in a circle facing inside (not necessarily in the same order) and playing a game of 'Passing the Buck'.
The game is played over 10 rounds. In each round, the child holding the Buck must pass it directly to a child sitting in one of the following positions:
• Immediately to the left;
• Immediate to the right;
• Second to the left; or
• Second to the right.
The game starts with Bina passing the Buck and ends with Chirag receiving the Buck. The table below provides some information about the pass types and the child receiving the Buck. Some information is missing and labelled as '?'.
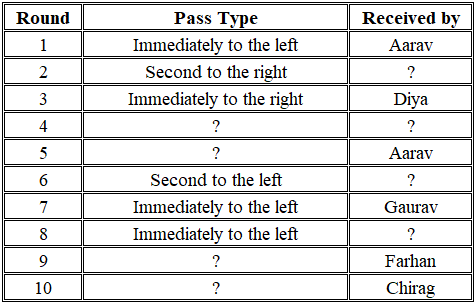
Question 5
Who is sitting immediately to the right of Bina?
correct answer:-2
Instruction for set 2:
Seven children, Aarav, Bina, Chirag, Diya, Eshan, Farhan, and Gaurav, are sitting in a circle facing inside (not necessarily in the same order) and playing a game of 'Passing the Buck'.
The game is played over 10 rounds. In each round, the child holding the Buck must pass it directly to a child sitting in one of the following positions:
• Immediately to the left;
• Immediate to the right;
• Second to the left; or
• Second to the right.
The game starts with Bina passing the Buck and ends with Chirag receiving the Buck. The table below provides some information about the pass types and the child receiving the Buck. Some information is missing and labelled as '?'.

Question 6
Who is sitting third to the left of Eshan?
correct answer:-3
Instruction for set 2:
Seven children, Aarav, Bina, Chirag, Diya, Eshan, Farhan, and Gaurav, are sitting in a circle facing inside (not necessarily in the same order) and playing a game of 'Passing the Buck'.
The game is played over 10 rounds. In each round, the child holding the Buck must pass it directly to a child sitting in one of the following positions:
• Immediately to the left;
• Immediate to the right;
• Second to the left; or
• Second to the right.
The game starts with Bina passing the Buck and ends with Chirag receiving the Buck. The table below provides some information about the pass types and the child receiving the Buck. Some information is missing and labelled as '?'.

Question 7
For which of the following pass types can the total number of occurrences be uniquely determined?
correct answer:-3
Instruction for set 2:
Seven children, Aarav, Bina, Chirag, Diya, Eshan, Farhan, and Gaurav, are sitting in a circle facing inside (not necessarily in the same order) and playing a game of 'Passing the Buck'.
The game is played over 10 rounds. In each round, the child holding the Buck must pass it directly to a child sitting in one of the following positions:
• Immediately to the left;
• Immediate to the right;
• Second to the left; or
• Second to the right.
The game starts with Bina passing the Buck and ends with Chirag receiving the Buck. The table below provides some information about the pass types and the child receiving the Buck. Some information is missing and labelled as '?'.

Question 8
For which of the following children is it possible to determine how many times they received the Buck?
correct answer:-4
CAT 2024 Arrangement questions
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.
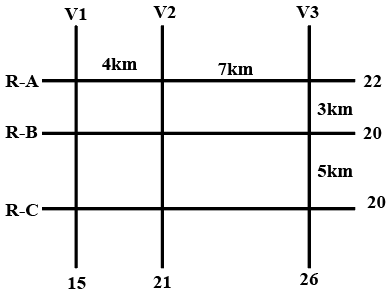
Question 1
Which of the following statements is correct?
correct answer:-2
Instruction for set 1:
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.

Question 2
How many ATMs have cash requirements of Rs. 10 Lakhs or more?
correct answer:-3
Instruction for set 1:
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.

Question 3
Which of the following two statements is/are DEFINITELY true?
Statement A: Each of R-A, R-B, and R-C has two ATMs.
Statement B: Each of V1, V2, and V3 has two ATMs.
correct answer:-1
Instruction for set 1:
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.

Question 4
What best can be said about the road distance (in km) between the ATMs having the second highest and the second lowest cash requirements?
correct answer:-4
Instruction for set 1:
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections.Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.

Question 5
What is the number of ATMs whose locations and cash requirements can both be uniquely determined?
correct answer:-3
CAT 2023 Arrangement questions
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Question 1
How many houses are vacant in Block XX?
correct answer:-3
Instruction for set 1:
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Question 2
Which of the following houses is definitely occupied?
correct answer:-3
Instruction for set 1:
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Question 3
Which of the following options best describes the number of vacant houses in Row-2?
correct answer:-4
Instruction for set 1:
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Question 4
What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
correct answer:-21
Instruction for set 1:
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count). The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Question 5
Which house in Block YY has parking space?
correct answer:-1
CAT 2020 Arrangement questions
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1, 3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Question 1
Initially cars numbered 1, 2, 3, and 4 arrive among which 1 and 4 are SUVs while 2 and 3 are compact cars. Car 1 then leaves, followed by the arrivals of car 5 (a compact car) and car 6 (an SUV). Car 4 then leaves. Then car 7 (an SUV) and car 8 (a compact car) arrive. At this moment, which among the following numbered car is parked next to car 3?
correct answer:-4
Instruction for set 1:
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1, 3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Question 2
Suppose eight cars have arrived, of which two have left. Also suppose that car 4 is a compact and car 7 is an SUV. Which of the following is a POSSIBLE current configuration of the parking lot?
correct answer:-4


