Let P$$_{1}$$ be the circle of radius R. A square Q$$_{1}$$ is inscribed in P$$_{1}$$ such that all the vertices of the square Q$$_{1}$$ lie on the circumference of P$$_{1}$$. Another circle P$$_{2}$$ is inscribed in Q$$_{1}$$. Another Square Q$$_{2}$$ is inscribed in the circle P$$_{2}$$. Circle P$$_{3}$$ is inscribed in the square Q$$_{2}$$ and so on. If S$$_{N}$$ is the area between Q$$_{N}$$ and P$$_{N+1}$$, where N represents the set of natural numbers, then the ratio of sum of all such S$$_{N}$$ to that of the area of the square Q$$_{1}$$ is :

Let us draw the diagram according to the information given,

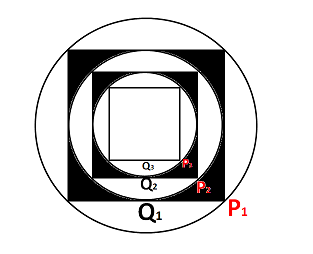
There will be infinite shaded areas as shown in the figure. 

Area of circle P$$_{1}$$ = $$\pi*R^2$$

Area of square Q$$_{1}$$ = $$(\sqrt{2}*R)^2$$ = $$2R^2$$

Area of circle P$$_{2}$$ = $$\pi*(\dfrac{R}{\sqrt{2}})^2=\pi*R^2/2$$

Area of square Q$$_{2}$$ = $$R^2$$

Area of circle P$$_{3}$$ = $$\pi*(\dfrac{R}{2})^2=\pi*R^2/4$$

Therefore, S$$_{N}$$ = [$$2R^2-\pi*\dfrac{R^2}{2}$$]+[$$R^2-\pi*\dfrac{R^2}{4}$$]+... 

S$$_{N}$$ = $$(2R^2+R^2+\dfrac{R^2}{2}+... )$$- $$(\pi*\dfrac{R^2}{2}+\pi*\dfrac{R^2}{4}+\pi*\dfrac{R^2}{8}...)$$

S$$_{N}$$ = $$4R^2-\pi*R^2$$

Therefore, $$\dfrac{S_{N}}{Q_{1}}$$ = $$\dfrac{4R^2-\pi*R^2}{2R^2}$$ = $$\dfrac{4 - \pi}{2}$$. Hence, option A is the correct answer.