In a circle, the height of an arc is 21 cm and the diameter is 84 cm. Find the chord of ‘half of the arc’

Let ABC be the arc as shown in the figure. It is known that the diameter of the circle = 84 cm. Hence, the radius of the circle = 42 cm. 

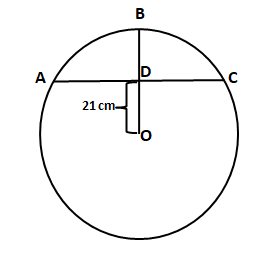
We can see that both CO and BO are equivalent to the radius of the circle. Hence, CO = 42 cm and BD = BO - OD = 42 - 21 = 21 cm. 

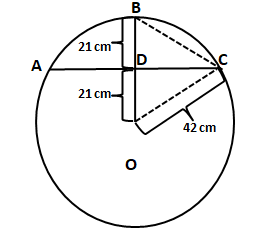
In triangle ODC, $$cosDOC = \dfrac{21}{42}$$

Hence, $$\angle$$ DOC = 60°

In triangle BOC, OB = OC. Hence, we can say that $$\angle$$ OCB = $$\angle$$ OBC = 60°.

Therefore, OBC is an equilateral triangle. Hence, OB = OC = BC = 42 cm. 

Hence, we can say that the length of the chord of ‘half of the arc’ = 42 cm. Therefore, option C is the correct answer.