A student who gets 20% marks fails by 20 marks, but another student who gets 36% marks gets 44 marks more than minimum passing marks. Find the maximum number of marks and percentage necessary for passing.
Solution
Let the maximum number of marks be 'x' and minimum passing marks be 'y'.
Given, A student who gets 20% marks fails by 20 marks.
$$\Rightarrow \frac{20}{100}\times x = y - 20$$
$$\Rightarrow 20x = 100y - 2000$$.................(1)
Also given that, another student who gets 36% marks gets 44 marks more than minimum passing marks.
$$\Rightarrow \frac{36}{100}\times x = y + 44$$
$$\Rightarrow 36x = 100y + 4400$$....................(2)
(2) - (1) $$\Rightarrow$$ 16x = 6400
$$\Rightarrow$$ x = 400
From (1) or (2), we get y = 100
Hence, maximum number of marks = x = 400
Percentage necessary for passing = $$\frac{y}{x}\times 100$$ = 25%
Video Solution
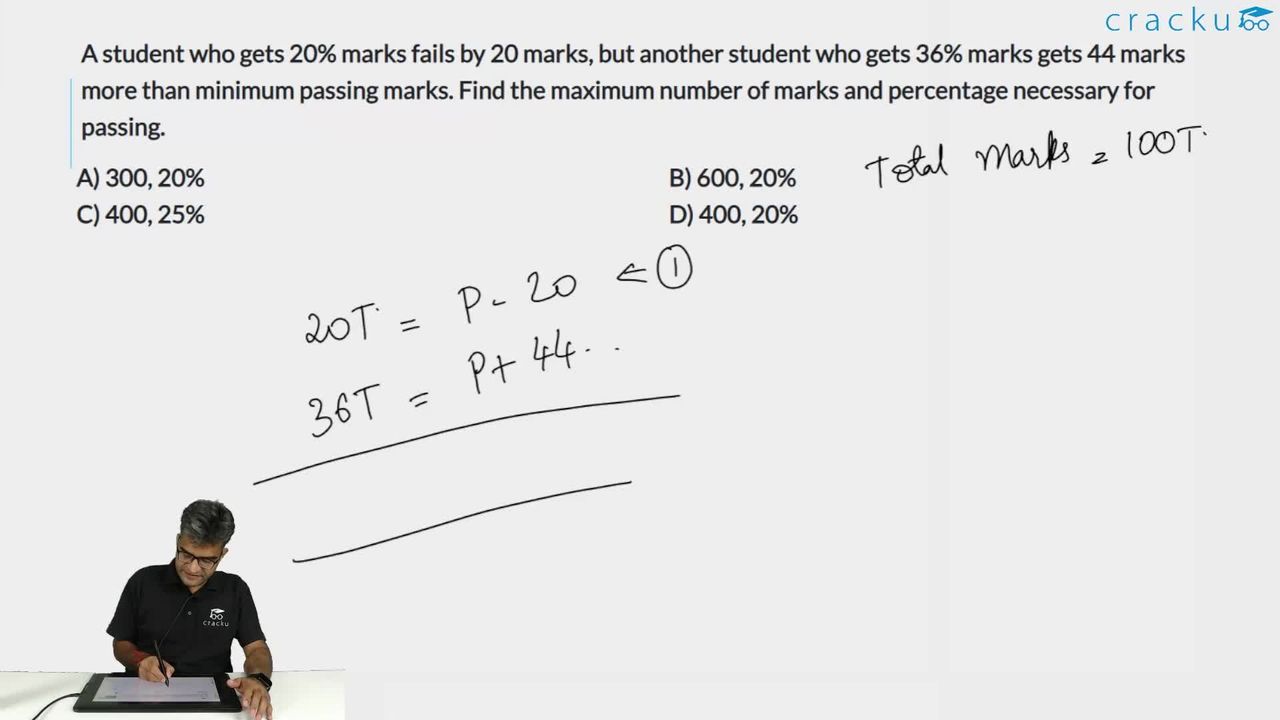
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 40+ previous papers with detau solutions PDF
- Top 500 MBA exam Solved Questions for Free

