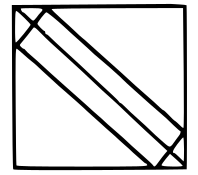
A rectangular plank $$\sqrt{10}$$ metre wide, is placed symmetrically along the diagonal of a square of side 10 metres as shown in the figure. The area of the plank is:

In the given diagram AB=$$\sqrt{10}$$ m

                          

Given that PQRS is a square and the plank is placed symmetrically $$\triangle$$BPA and $$\triangle$$AQC will be isosceles right triangles.

Hence $$\text{AB}^2 = \text{PA}^2 + \text{PB}^2$$

As the plank is symmetrical, PA = PB, 

Hence $$\text{AB}^2 = 2\times\text{PA}^2$$  =>  $$\sqrt{10}^2 = 2\times\text{PA}^2$$

          So PA=PB=$$\sqrt{\frac{10}{2}}$$=$$\sqrt{5}$$ m

          PQ = PA+AQ  

          AQ = PQ-PA = 10-$$\sqrt{5}$$ m

We know that AQ=QC ($$\triangle$$AQC is isosceles right triangle)

     So AC=$$\sqrt{2}$$AQ=$$\sqrt{2}$$*(10-$$\sqrt{5}$$) m

Now we can calculate area of plank 

     Area of ABCD= AB*AC= $$\sqrt{10}$$*$$\sqrt{2}$$(10-$$\sqrt{5}$$)=10($$\sqrt{20}$$-1) sq. mt