The product of the roots of the equation $$\sqrt[3]{11+2x}+\sqrt[3]{11-2x}=2$$ is approximately equal to:
Solution
Cubing the given equation, we have :
$$\left(a+b\right)^3=\ a^3+\ b^3+3\cdot a\cdot b\left(a+b\right)$$
$$11+2x+11-2x+3\cdot\left(11+2x\right)^{\frac{1}{3}}\left(11-2x\right)^{\frac{1}{3}}\left(a+b\right)$$
Given a+b = 2.
Hence :
22 + $$3\cdot\left(11+2x\right)^{\frac{1}{3}}\left(11-2x\right)^{\frac{1}{3}}\left(2\right)$$
= 22 + 6*($$\left(121-4x^2\right)^{\frac{1}{3}}$$) = 8
Cubing this we get: $$121-4x^2=-\frac{343}{27}$$
$$4x^2=\ 121+\frac{343}{27}=\ \frac{3610}{27}$$
$$x^2\ =\ 33.42$$
One root would be $$ +\sqrt{33.42}$$ and the other would be $$-\sqrt{33.42}$$.
The product of the roots would be approximately -33.
Video Solution
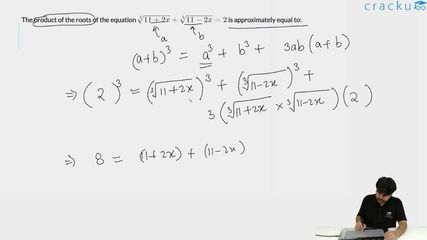
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 170+ previous papers with solutions PDF
- Top 5000+ MBA exam Solved Questions for Free

