Question 27

In a rocket shape firecracker, explosive powder is to be filled up inside the metallic enclosure. The metallic enclosure is made up of a cylindrical base and conical top with the base of radius 8 centimeter. The ratio of height of cylinder and cone is 5:3. A cylindrical hole is drilled through the metal solid with height one third the height of the metal solid. What should be the radius of the hole, so that volume of the hole (in which gun powder is to be filled up) is half of the volume of metal solid after drilling?

Solution

Let us draw an appropriate diagram. Let us assume that 'R' is the radius of the hole.

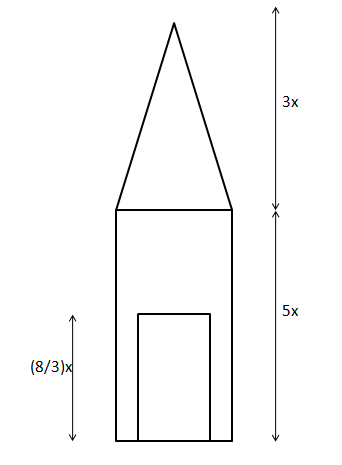
$$\dfrac{1}{2}$$*(Total volume - Volume of the hole) = Volume of the hole

Volume of the hole = $$\dfrac{1}{3}*\text{Total volume of the rocket}$$

$$\pi*R^2*(8/3)x$$ = $$\dfrac{1}{3}*(\pi*8^2*5x+\dfrac{1}{3}*\pi*8^2*3x)$$

$$R^2*(8/3)$$ = $$\dfrac{1}{3}*(8^2*5+\dfrac{1}{3}*8^2*3)$$

$$R^2 = 48$$

$$R$$ = $$4\sqrt{3}$$ cm. Hence, option A is the correct answer.

Create a FREE account and get:

CAT Quant Questions | CAT Quantitative Ability