Mukesh, Suresh and Dinesh travel from Delhi to Mathura to attend Janmasthmi Utsav. They have a bike which can carry only two riders at a time as per traffic rules. Bike can be driven only by Mukesh. Mathura is 300Km from Delhi. All of them can walk at 15Km/Hrs. All of them start their journey from Delhi simultaneously and are required to reach Mathura at the same time. If the speed of bike is 60Km/Hrs then what is the shortest possible time in which all three can reach Mathura at the same time.

Let us assume that Mukesh and Suresh started on bike from Delhi to Mathura and Dinesh started walking at the same time. Mukesh drops Suresh in a mid-way such that Suresh will take same time to reach Mathura with Mukesh and Dinesh. In the same time Mukesh will turn back and will pick up Dinesh. 

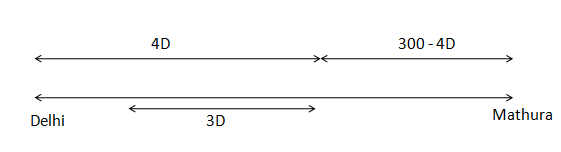
Let us assume that '4D' is the distance covered by by Mukesh and Suresh. Then Suresh must have covered remaining 300 - 4D kms by walking at 15 km/hr. When Mukesh dropped Suresh by that time Dinesh have already covered D kms and now Mukesh and Dinesh and would have 3D kms apart. Since Mukesh is 4 times faster than Dinesh, Mukesh would have covered (4/5) of 3D kms. 

In addition to this, Mukesh and Dinesh have to cover 2.4D+300-4D kms to reach Mathura at 60 km/hr.

By equating the time taken by Mukesh and Suresh to reach Mathura after the point when Mukesh dropped Suresh,

$$\dfrac{300-4D}{15}=\dfrac{2.4D+2.4D+300-4D}{60}$$

$$\Rightarrow$$ 16.8*D = 900

$$\Rightarrow$$ D = $$\dfrac{375}{7}$$ kms

Therefore, minimum time taken by them to finish the journey = $$\dfrac{4D}{60}+\dfrac{300-4D}{15}$$

$$\Rightarrow$$ $$20 - \dfrac{D}{5}$$

$$\Rightarrow$$ $$20 - \dfrac{375}{7*5}$$

$$\Rightarrow$$ $$20 - \dfrac{75}{7}$$

$$\Rightarrow$$ $$\dfrac{65}{7}$$ or $$9\dfrac{2}{7}$$ hours. Hence, option B is the correct answer.