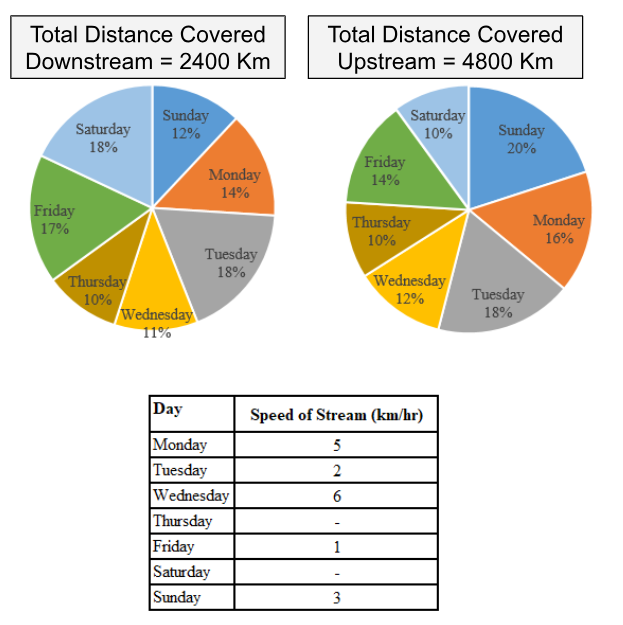
If the time taken by boat to travel upstream on Monday is $$27\dfrac{1}{5}$$ hrs. more than the time taken by it to travel downstream on the same day, then find the speed of boat in still water on Monday ?(speed of boat in still water is same in upstream as in downstream)

Distance travelled on Monday = 14% of 2400, i.e. 336 km Downstream and 16% of 4800, i.e. 768 Km Upstream.

It is given that the time taken for upstream travel was 27.2 hours more than for downstream.

Let x be the speed of the boat in still water

So, we can say:

$$\dfrac{768}{x-5}=\dfrac{336}{x+5}+27.2$$

$$\dfrac{768(x+5)-336(x-5)}{(x-5)(x+5)}=27.2$$

$$\dfrac{768x+3840-336x+1680}{x^2-25}=27.2$$

$$\dfrac{432x+5520}{x^2-25}=27.2$$

Upon simplifying, we get the following quadratic equation:

$$17x^2-270x-3875=0$$

$$x = \dfrac{270 \pm \sqrt{(-270)^2-4(17)(-3875)}}{2(17)}$$

$$x = \dfrac{270 \pm \sqrt{72900+263500}}{34}$$

$$x = \dfrac{270 \pm \sqrt{336400}}{34}$$

The only positive solution for x = 25.