Instructions

Study the data given below and answer the following questions. The pie charts shown below shows the distance covered by a boat moving upstream and downstream indifferent days of a week. And the table shows the speed of stream in km/hr. in different days of a week.

Question 3

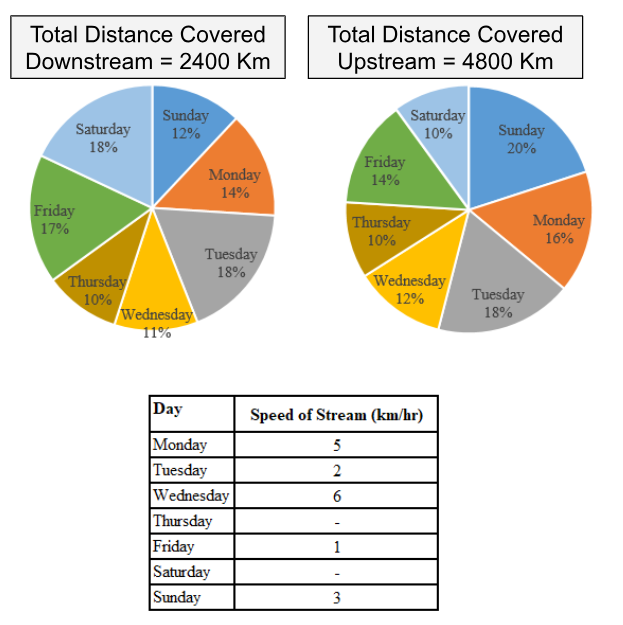
If the speed of boat in still water on Saturday was 27 km/hr and the speed of boat in still water on Wednesday was $$66\dfrac{2}{3}\%$$ more than that of Saturday and time taken to travel upstream on Wednesday is $$\dfrac{16}{13}$$ times than time taken by it to travel downstream on Saturday, then find the speed of stream (in kmph) on Saturday?

Solution

Distance upstream (Wednesday): 12% of 4800 km = 576 km.

The speed of the boat in still water (Wednesday) is 66.67% which is 2/3 more than on Saturday: $$27\times\left(1+\dfrac{2}{3}\right)=45\ kmph$$

Upstream speed (Wednesday) = Speed of boat - Speed of stream = 45 − 6 = 39 kmph

Time taken upstream (Wednesday) = $$\dfrac{576}{39\ }=\dfrac{192}{39}\ hrs$$

We are given that the upstream time on Wednesday is 16/13 times the downstream time on Saturday.

$$\dfrac{192}{13}=\dfrac{16}{13}\times Downstream\ Time$$

So, downstream time: 12 hours

Downstream speed (Saturday): 432/12 = 36 kmph

Since the downstream speed is the sum of the boat's speed in still water and the stream's speed.

36 kmph = 27 kmph+Speed of stream

Speed of stream (Saturday): 36−27 = 9 kmph

View More Questions From Temporary

Create a FREE account and get:

Download Maths Shortcuts PDF
Get 300+ previous papers with solutions PDF
500+ Online Tests for Free

maruti sir image

MAT Quant Questions | MAT Quantitative Ability

MAT Time Speed Distance Questions MAT Venn Diagrams Questions MAT Remainders Questions MAT Profit and Loss Questions MAT Data Sufficiency Questions MAT Percentages Questions MAT Linear Equations Questions MAT Quadratic Equations Questions MAT Coordinate Geometry Questions MAT Algebra Questions MAT Averages Mixtures Alligations Questions MAT Number Systems Questions MAT Time And Work Questions MAT Logarithms Questions MAT Averages Questions MAT Number Series Questions MAT Probability, Combinatorics Questions MAT Inequalities Questions MAT Functions, Graphs and Statistics Questions MAT Logarithms, Surds and Indices Questions MAT Arithmetic Questions MAT Geometry Questions MAT Time, Speed and Distance Questions MAT Averages, Ratio and Proportion Questions MAT Progressions and Series Questions MAT Profit And Loss Questions MAT Mensuration Questions MAT Simple Interest Compound Interest Questions

MAT DILR Questions | LRDI Questions For MAT

MAT Quant Based LR Questions MAT Data Interpretation Questions MAT Maxima-Minima Questions MAT Selection With Condition Questions MAT Table based DI Sets Questions MAT Miscellaneous LR Questions MAT 2D & 3D LR Questions MAT Games and Tournamnents Questions MAT DI with connected data sets Questions MAT Venn Diagrams Questions MAT Charts Questions MAT DI Miscellaneous Questions MAT Puzzles Questions MAT Routes And Networks Questions MAT Scheduling Questions MAT Truth Lie Concept Questions MAT Data change over a period Questions MAT Special Charts Questions MAT Data Interpretation Basics Questions MAT Quant Based DI Questions MAT Coins and Weights Questions MAT Arrangement Questions

MAT Verbal Ability Questions | VARC Questions For MAT

MAT Para Jumbles Questions MAT Vocabulary Questions MAT Para Summary Questions MAT Critical Reasoning Questions MAT Reading Comprehension Questions MAT Odd One Out Questions MAT Grammar and Sentence Correction Questions MAT Verbal Ability Questions MAT Miscellaneous Questions