Question 19

A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60 degrees. When he retires 'y' metre from the bank perpendicular to the tree, he finds the angle to be 45 degrees. When he further retires $$15 - 5\sqrt{3}$$ metre perpendicular to the tree, he finds the angle to be 30 degrees. Find the height of the tree in metres?

Solution

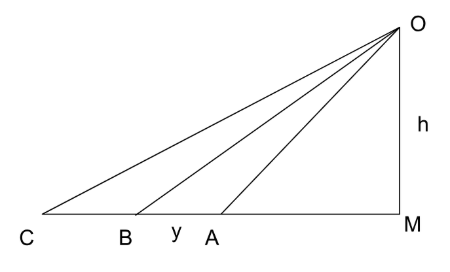
It is given that $$\angle\ OAM=60^{\circ\ },\ \angle\ OBM=45^{\circ},\ \angle\ OCM=30^{\circ\ },\ AB=y,\ BC=15-5\sqrt{\ 3}\ $$

Let the height of the tree be OM = $$'h'$$.

Then $$AM\ =\dfrac{OM}{\tan\ 60^{\circ\ }}=\dfrac{h}{\sqrt{\ 3}}$$

From $$\triangle\ OBM,\ \tan\ 45^{\circ\ }=\dfrac{h}{\dfrac{h}{\sqrt{\ 3}}+y}$$

$$\dfrac{h}{\sqrt{\ 3}}+y=h$$

$$y=h-\dfrac{h}{\sqrt{\ 3}}$$

From $$\triangle\ OCM,\ \tan30^{\circ\ }=\dfrac{h}{15-5\sqrt{\ 3}+y+\dfrac{h}{\sqrt{\ 3}}}$$

$$\dfrac{1}{\sqrt{\ 3}}=\dfrac{h}{15-5\sqrt{\ 3}+h-\dfrac{h}{\sqrt{\ 3}}+\dfrac{h}{\sqrt{\ 3}}}$$

$$\dfrac{1}{\sqrt{\ 3}}=\dfrac{h}{15-5\sqrt{\ 3}+h}$$

$$15-5\sqrt{\ 3}+h=h\sqrt{\ 3}$$

$$15-5\sqrt{\ 3}=h\left(\sqrt{\ 3}-1\right)$$

$$h=\dfrac{15-5\sqrt{\ 3}}{\left(\sqrt{\ 3}-1\right)}$$

$$h=\dfrac{5\sqrt{\ 3}\times\ \left(\sqrt{\ 3}-1\right)}{\left(\sqrt{\ 3}-1\right)}=5\sqrt{\ 3}$$

Option (C) is the answer.

Share on Whatsapp Share on Whatsapp

Create a FREE account and get:

Drop Your File Here!