If $$\frac{(a + b)}{c} = \frac{6}{5}$$ and $$\frac{(b + c)}{a} = \frac{9}{2}$$, then what is the value of $$\frac{(a + c)}{b}$$?
Solution
$$\frac{(a + b)}{c} = \frac{6}{5}$$
5a+5b=6c
$$\frac{(b + c)}{a} = \frac{9}{2}$$
2b+2c=9a
9a-2b=2c
27a-6b=6c
5a+5b=6c
27a-6b=5a+5b
22a=11b
b=2a
4a+2c=9a
2c=5a
c=(5/2)a
$$\frac{(a + c)}{b}$$
=((a+(5/2)a))/2a
=7a/4a
=7/4
Video Solution
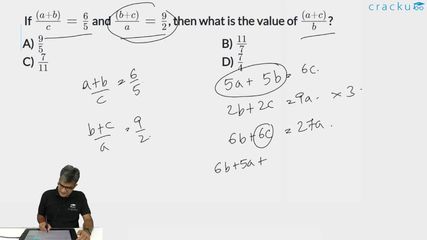
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

