XAT 2015 Question Paper - QUANT
For the following questions answer them individually
XAT 2015 - QUANT - Question 52
What is the sum of the following series?
-64, -66, -68,............., -100
XAT 2015 - QUANT - Question 53
A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re - cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?
XAT 2015 - QUANT - Question 54
The Maximum Retail Price (MRP) of a product is 55% above its manufacturing cost. The product is sold through a retailer, who earns 23% profit on his purchase price. What is the profit percentage (expressed in nearest integer) for the manufacturer who sells his product to the retailer? The retailer gives 10% discount on MRP.
XAT 2015 - QUANT - Question 55
Ramesh plans to order a birthday gift for his friend from an online retailer. However, the birthday coincides with the festival season during which there is a huge demand for buying online goods and hence deliveries are often delayed. He estimates that the probability of receiving the gift, in time, from the retailers A, B, C and D would be 0.6, 0.8, 0.9 and 0.5 respectively.
Playing safe, he orders from all four retailers simultaneously. What would be the probability that his friend would receive the gift in time?
XAT 2015 - QUANT - Question 56
The figure below has been obtained by folding a rectangle. The total area of the figure (as visible) is 144 square meters. Had the rectangle not been folded, the current overlapping part would have been a square. What would have been the total area of the original unfolded rectangle?
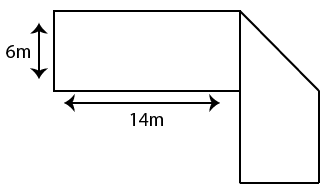
XAT 2015 - QUANT - Question 57
Find the equation of the graph shown below.

XAT 2015 - QUANT - Question 58
Product M is produced by mixing chemical X and chemical Y in the ratio of 5 : 4. Chemical X is prepared by mixing two raw materials, A and B, in the ratio of 1 : 3. Chemical Y is prepared by mixing raw materials, B and C, in the ratio of 2 : 1. Then the final mixture is prepared by mixing 864 units of product M with water. If the concentration of the raw material B in the final mixture is 50%, how much water had been added to product M?
XAT 2015 - QUANT - Question 59
A circular road is constructed outside a square field. The perimeter of the square field is 200 ft. If the width of the road is 7√2 ft. and cost of construction is Rs. 100 per sq.ft. Find the lowest possible cost to construct 50% of the total road.
XAT 2015 - QUANT - Question 60
In the diagram below, CD = BF = 10 units and ∠CED = ∠BAF = 30°. What would be the area of triangle AED? (Note: Diagram below may not be proportional to scale.)

XAT 2015 - QUANT - Question 61
Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.
XAT 2015 - QUANT - Question 62
If $$f(x^2 - 1) = x^4 - 7x^2 + k_1$$ and $$f(x^3 - 2) = x^6 - 9x^3 +k_2$$ then the value of $$(k_2 - k_1)$$ is
XAT 2015 - QUANT - Question 63
In the beginning of the year 2004, a person invests some amount in a bank. In the beginning of 2007, the accumulated interest is Rs. 10,000 and in the beginning of 2010, the accumulated interest becomes Rs. 25,000. The interest rate is compounded annually and the annual interest rate is fixed. The principal amount is:
XAT 2015 - QUANT - Question 64
The tax rates for various income slabs are given below.

There are 15 persons working in an organization. Out of them, 3 to 5 persons are falling in each of the income slabs mentioned above. Which of the following is the correct tax range of the 15 persons? (E.g. If one is earning Rs. 2000, the tax would be:
500 × 0 + 1500 ×0.05)
XAT 2015 - QUANT - Question 65
If a, b, c and d are four different positive integers selected from 1 to 25, then the highest possible value of ((a + b) + (c +d ))/((a + b) + (c - d)) would be:
XAT 2015 - QUANT - Question 66
An ascending series of numbers satisfies the following conditions:
i. When divided by 3, 4, 5 or 6, the numbers leave a remainder of 2.
Ii. When divided by 11, the numbers leave no remainder.
The 6th number in this series will be:
XAT 2015 - QUANT - Question 67
In an examination, two types of questions are asked: one mark questions and two marks questions. For each wrong answer, of one mark question, the deduction is 1/4 of a mark and for each wrong answer, of two marks question, the deduction is 1/3 of a mark.
Moreover, 1/2 of a mark is deducted for any unanswered question. The question paper has 10 one mark questions and 10 two marks questions. In the examination, students got all possible marks between 25 and 30 and every student had different marks. What would be the rank of a student, who scores a total of 27.5 marks?
XAT 2015 - QUANT - Question 68
For a positive integer x, define f(x) such that f(x + a) = f(a × x), where a is an integer and f(1) = 4. If the value of f(1003) = k, then the value of ‘k’ will be:
XAT 2015 - QUANT - Question 69
Devanand’s house is 50 km West of Pradeep’s house. On Sunday morning, at 10 a.m., they leave their respective houses.
Under which of the following scenarios, the minimum distance between the two would be 40 km?
Scenario I: Devanand walks East at a constant speed of 3 km per hour and Pradeep walks South at a constant speed of 4 km per hour.
Scenario II: Devanand walks South at a constant speed of 3 km per hour and Pradeep walks East at a constant speed of 4 km per hour.
Scenario III: Devanand walks West at a constant speed of 4 km per hour and Pradeep walks East at a constant speed of 3 km per hour.
XAT 2015 - QUANT - Question 70
The median of 11 different positive integers is 15 and seven of those 11 integers are 8, 12, 20, 6, 14, 22, and 13.
Statement I: The difference between the averages of four largest integers and four smallest integers is 13.25.
Statement II: The average of all the 11 integers is 16.
Which of the following statements would be sufficient to find the largest possible integer of these numbers?
XAT 2015 - QUANT - Question 71
The parallel sides of a trapezoid ABCD are in the ratio of 4 : 5. ABCD is divided into an isosceles triangle ABP and a parallelogram PBCD (as shown below). ABCD has a perimeter equal to 1120 meters and PBCD has a perimeter equal to 1000 meters. Find Sin$$\angle$$ABC, given 2$$\angle$$DAB = $$\angle$$BCD.
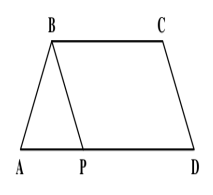
XAT 2015 - QUANT - Question 72
A three - digit number has digits in strictly descending order and divisible by 10. By changing the places of the digits a new three - digit number is constructed in such a way that the new number is divisible by 10. The difference between the original number and the new number is divisible by 40. How many numbers will satisfy all these conditions?
XAT 2015 - QUANT - Question 73
The centre of a circle inside a triangle is at a distance of 625 cm from each of the vertices of the triangle. If the diameter of the circle is 350 cm and the circle is touching only two sides of the triangle, find the area of the triangle.
XAT 2015 - QUANT - Question 74
If the last 6 digits of [(M)! - (N)!] are 999000, which of the following option is not possible for (M) × (M - N)? Both (M) and (N) are positive integers and M > N. (M)! is factorial M.
XAT 2015 - QUANT - Question 75
A person is standing at a distance of 1800 meters facing a giant clock at the top of a tower. At 5.00 p.m., he can see the tip of the minute hand of the clock at 30 degree elevation from his eye - level. Immediately, the person starts walking towards the tower. At 5.10 pm., the person noticed that the tip of the minute hand made an angle of 60 degrees with respect to his eye - level. Using three - dimensional vision, find the speed at which the person is walking. The length of the minutes hand is 200√3 meters (√3 = 1.732).
XAT 2015 - QUANT - Question 76
Three pipes are connected to an inverted cone, with its base at the top. Two inlet pipes, A and B, are connected to the top of the cone and can fill the empty in 8 hours and 12 hours, respectively. The outlet pipe C, connected to the bottom, can empty a filled cone in 4 hours. When the cone is completely filled with water, all three pipes are opened. Two of the three pipes remain open for 20 hours continuously and the third pipe remains open for a lesser time. As a result, the height of the water inside the cone comes down to 50%. Which of the following options would be possible?
Answer the questions on the basis of information given below.
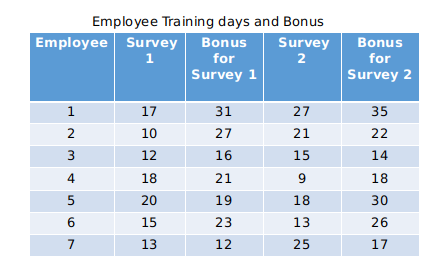
As a part of employee improvement programs, every year an organization conducts a survey on three factors: 1. Number of days (in integers) of training undergone, 2. Amount of bonus (in lacs) received by an employee and 3. Employee effectiveness score (on the scale of 1 to 10). Survey results for last two years are given below for the same seven employees.





XAT 2015 - QUANT - Question 77
In Survey 1, what was the average bonus earned by employees who underwent training for more than 17 days?
XAT 2015 - QUANT - Question 78
Identify the number of employees whose employee effectiveness score was higher than 7 in Survey 1, but whose bonus was lower than 20 lacs in Survey 2.
XAT 2015 - QUANT - Question 79
From Survey 1 to Survey 2, how many employees underwent more days of training but their annual bonus decreased?
XAT 2015 - QUANT - Question 80
From Survey 1 to Survey 2: for how many employees training days increased along with an increase of employee effective score by at least 1.0 rating?
Answer the questions on the basis of information given below.
Twitter allows its users to post/share and read short messages known as tweets. Tweets can be of three types – Positive Tweets (in support), Negative Tweets (against) and Neutral Tweets. The following table presents the Number of Votes and Tweets received by certain political parties.
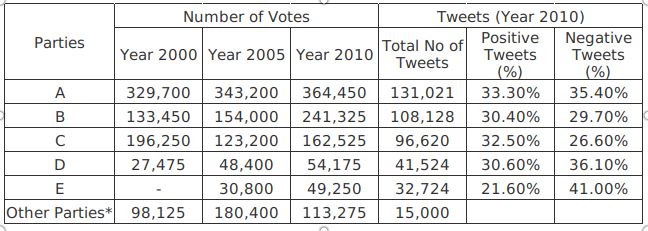
* Any party which has secured less than 2% of the total votes falls under ‘Other Parties’ category. For example, Party E secured less than 2% of total votes, in the year 2000.
Note: If the vote share (%age of total votes) of a party changes from 15% to 40%, gain in vote share would be 25% (= 40%, – 15%).
XAT 2015 - QUANT - Question 81
Which of the following options correctly arranges the political parties in descending order of gain in vote share from the year 2005 to the year 2010?
XAT 2015 - QUANT - Question 82
Which of the following parties received maximum number of “neutral tweets” in the year 2010?
XAT 2015 - QUANT - Question 83
Between 2000 and 2010, in terms of gain in vote share which of the following cannot
be a possible value (approximated to one decimal place) for any party?
XAT 2015 - QUANT - Question 84
In 2010, which of the following options has maximum difference between the vote share and tweet share?
Two Factor Authentication
Incase of any issue contact support@cracku.in












.png)
.png)
