The parallel sides of a trapezoid ABCD are in the ratio of 4 : 5. ABCD is divided into an isosceles triangle ABP and a parallelogram PBCD (as shown below). ABCD has a perimeter equal to 1120 meters and PBCD has a perimeter equal to 1000 meters. Find Sin$$\angle$$ABC, given 2$$\angle$$DAB = $$\angle$$BCD.
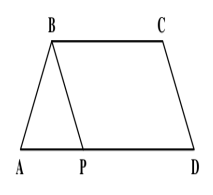
Solution
AB + BC + CD + AD = 1120 ------------Eqn(I)
PB + BC + CD + PD = 1000 -------------Eqn(II)
Subtracting eqn(II) from (I), we get :
=> AB - PB + (AD - PD) = 120
=> AB - PB + AP = 120
=> AB + AP = 120 + PB
Now, if AB = PB, => AP = 120
=> AD = 600 and BC = 480, then AB + PB + CD = 40, which is not possible (We know that BC = PD. If BC = PD = 480, then BC+PD = 960. PB + BC + CD + PD = 1000.
=> PB+CD = 40. Therefore, AB + PB+CD should be greater than 40).
Similarly, AB = AP is also not possible. Thus $$AP = BP$$

=> $$\angle ABC = x + (180 - 2x) = (180 - x)$$
=> $$sin \angle ABC = sin (180 - x) = sin x$$
Also, perimeter of PBCD = $$10y = 1000$$ => $$y = 100$$
and perimeter of ABCD = $$AB + 10y = 1120$$ => $$AB = 120$$
Applying cosine rule in $$\triangle$$ ABP
=> $$cos x = \frac{(AB)^2 + (AP)^2 - (BP)^2}{2 AB AP}$$
=> $$cos x = \frac{(120)^2 + (100)^2 - (100)^2}{2 \times 120 \times 100}$$
=> $$cos x = \frac{120}{200} = \frac{3}{5}$$
$$\therefore sin x = \sqrt{1 - (\frac{3}{5})^2} = \sqrt{1 - \frac{9}{25}}$$
= $$\sqrt{\frac{16}{25}} = \frac{4}{5}$$
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
