CAT 2024 Slot 1 Question Paper
Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D. The number of stars received by A and B from the six web surfers is shown in the figure below.
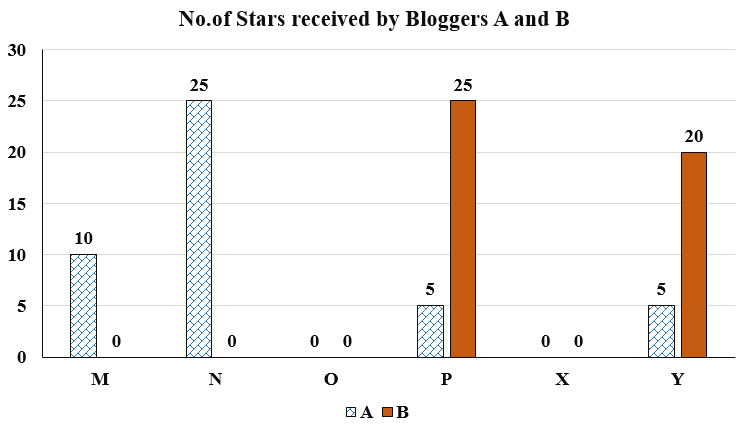
The following additional facts are known regarding the number of stars received by the bloggers from the surfers.
1. The numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0).
2. The total numbers of stars received by the bloggers were the same.
3. Each blogger received a different number of stars from M.
4. Two surfers gave all their stars to a single blogger.
5. D received more stars than C from Y.
CAT 2024 Slot 1 - Question 31
How many surfers distributed their stars among exactly 2 bloggers?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 32
Which of the following can be determined with certainty?
I. The number of stars received by C from M
II. The number of stars received by D from O
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
CAT 2024 Slot 1 - Question 33
How many rounds were there in the tournament?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 34
What is the number of the team that played Team 1 in Round 5?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 35
Which team among the teams numbered 2, 3, 4, and 5 was not part of the same group?
CAT 2024 Slot 1 - Question 36
What is the number of the team that played Team 1 in Round 7?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 37
What is the number of the team that played Team 6 in Round 3?
789
456
123
0.-
Clear All
Two students, Amiya and Ramya are the only candidates in an election for the position of class representative. Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
• The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. For example, if Amiya and Ramya both run vigorous campaigns, then 20 × (2+2)%, that is, 80% of the students will vote in the election.
• Among voting students, the percentage of votes for each candidate will be proportional to the levels of their campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2) campaign, then Amiya will receive 1/3 of the votes cast, and Ramya will receive the other 2/3. The above-mentioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
• If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then 10% of the students who would have otherwise voted for Amiya will vote for Ramya, and another 10% who would have otherwise voted for Amiya, will not vote at all.
• If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then 20% of the students who would have otherwise voted for Ramya will vote for Amiya, and another 5% who would have otherwise voted for Ramya, will not vote at all.
• If both run campaigns attacking each other, then 10% of the students who would have otherwise voted for them had they run campaigns focusing on issues, will not vote at all.
CAT 2024 Slot 1 - Question 38
If both of them run staid campaigns attacking the other, then what percentage of students will vote in the election?
CAT 2024 Slot 1 - Question 39
What is the minimum percentage of students who will vote in the election?
CAT 2024 Slot 1 - Question 40
If Amiya runs a campaign focusing on issues, then what is the maximum percentage of votes that she can get?
CAT Quant Questions | CAT Quantitative Ability
CAT DILR Questions | LRDI Questions For CAT
CAT Verbal Ability Questions | VARC Questions For CAT
Also Read
Frequently Asked Questions
You can download the CAT 2024 Slot 1 question paper PDF from Cracku’s official website, which also offers free memory-based questions and video solutions.
Yes, Cracku provides free video solutions for CAT 2024 Slot 1 questions, covering each section with expert explanations and tips.
Cracku’s video solutions are known for their accuracy, offering clear, step-by-step explanations based on memory-based questions shared by test-takers.
Reviewing Slot 1 helps you analyze the actual exam pattern, difficulty level, and question types. It’s a great way to prepare smarter for future CAT attempts.
Yes, the downloadable PDF from Cracku includes all three sections—VARC, DILR, and QA—as they appeared in the CAT 2024 Slot 1 exam.
Cracku’s video solutions offer expert strategies, tricks, and detailed explanations to help improve your accuracy, speed, and confidence in the exam.












