CAT 2024 Slot 1 Question Paper
Two students, Amiya and Ramya are the only candidates in an election for the position of class representative. Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
• The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. For example, if Amiya and Ramya both run vigorous campaigns, then 20 × (2+2)%, that is, 80% of the students will vote in the election.
• Among voting students, the percentage of votes for each candidate will be proportional to the levels of their campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2) campaign, then Amiya will receive 1/3 of the votes cast, and Ramya will receive the other 2/3. The above-mentioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
• If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then 10% of the students who would have otherwise voted for Amiya will vote for Ramya, and another 10% who would have otherwise voted for Amiya, will not vote at all.
• If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then 20% of the students who would have otherwise voted for Ramya will vote for Amiya, and another 5% who would have otherwise voted for Ramya, will not vote at all.
• If both run campaigns attacking each other, then 10% of the students who would have otherwise voted for them had they run campaigns focusing on issues, will not vote at all.
CAT 2024 Slot 1 - Question 41
If Ramya runs a campaign attacking Amiya, then what is the minimum percentage of votes that she is guaranteed to get?
CAT 2024 Slot 1 - Question 42
What is the maximum possible voting margin with which one of the candidates can win?
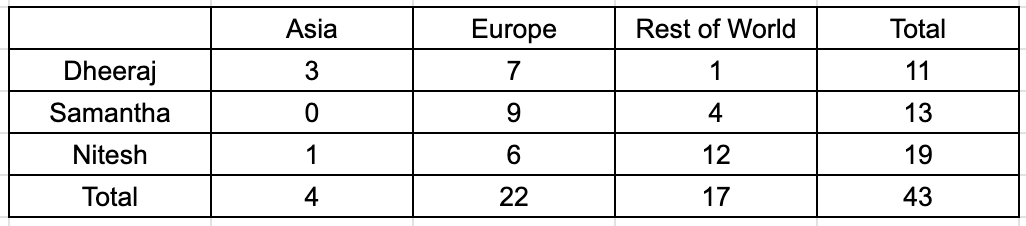
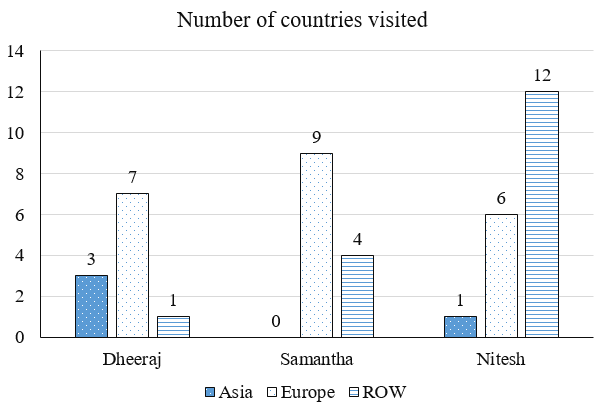
The chart below provides complete information about the number of countries visited by Dheeraj, Samantha and Nitesh, in Asia, Europe and the rest of the world (ROW).
The following additional facts are known about the countries visited by them.
1. 32 countries were visited by at least one of them.
2. USA (in ROW) is the only country that was visited by all three of them.
3. China (in Asia) is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha.
4. France (in Europe) is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh.
5. Half of the countries visited by both Samantha and Nitesh are in Europe.
CAT 2024 Slot 1 - Question 43
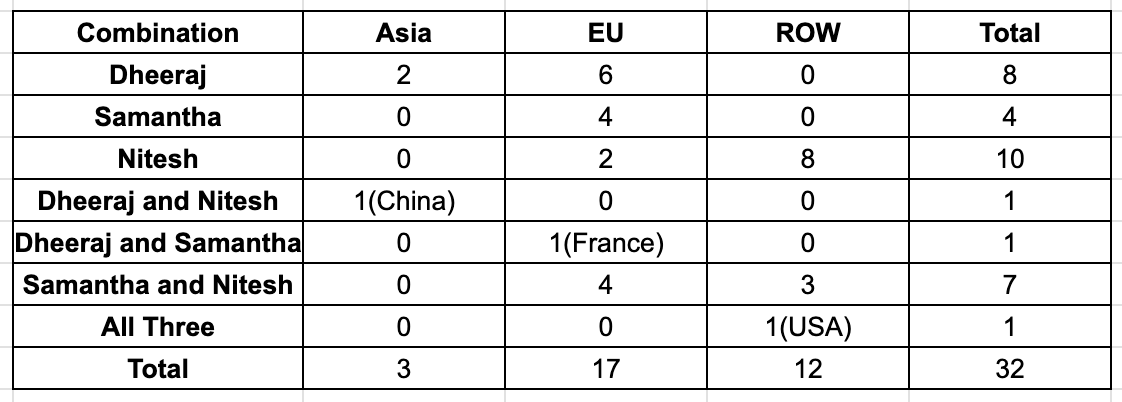
How many countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 44
How many countries in Europe were visited only by Nitesh?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 45
How many countries in the ROW were visited by both Nitesh and Samantha?
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 46
How many countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh?
For the following questions answer them individually
CAT 2024 Slot 1 - Question 47
Consider two sets $$A = \left\{2, 3, 5, 7, 11, 13 \right\}$$ and $$B = \left\{1, 8, 27 \right\}$$. Let f be a function from A to B such that for every element in B, there is at least one element a in A such that $$f(a) = b$$. Then, the total number of such functions f is
CAT 2024 Slot 1 - Question 48
Let $$x, y,$$ and $$z$$ be real numbers satisfying
$$4(x^{2}+y^{2}+z^{2})=a,$$
$$4(x-y-z)=3+a$$
The a equals
CAT 2024 Slot 1 - Question 49
lf the equations $$x^{2}+mx+9=0, x^{2}+nx+17=0$$ and $$x^{2}+(m+n)x+35=0$$ have a common negative root, then the value of $$(2m+3n)$$ is
789
456
123
0.-
Clear All
CAT 2024 Slot 1 - Question 50
Suppose $$x_{1},x_{2},x_{3},...,x_{100}$$ are in arithmetic progression such that $$x_{5}=-4$$ and $$2x_{6}+2x_{9}=x_{11}+x_{13}$$, Then,$$x_{100}$$ equals
CAT Quant Questions | CAT Quantitative Ability
CAT DILR Questions | LRDI Questions For CAT
CAT Verbal Ability Questions | VARC Questions For CAT
Also Read
Frequently Asked Questions
You can download the CAT 2024 Slot 1 question paper PDF from Cracku’s official website, which also offers free memory-based questions and video solutions.
Yes, Cracku provides free video solutions for CAT 2024 Slot 1 questions, covering each section with expert explanations and tips.
Cracku’s video solutions are known for their accuracy, offering clear, step-by-step explanations based on memory-based questions shared by test-takers.
Reviewing Slot 1 helps you analyze the actual exam pattern, difficulty level, and question types. It’s a great way to prepare smarter for future CAT attempts.
Yes, the downloadable PDF from Cracku includes all three sections—VARC, DILR, and QA—as they appeared in the CAT 2024 Slot 1 exam.
Cracku’s video solutions offer expert strategies, tricks, and detailed explanations to help improve your accuracy, speed, and confidence in the exam.