CAT 2020 Slot 1 Question Paper
For the following questions answer them individually
CAT 2020 Slot 1 - Question 51
If Y is a negative number such that $$2^{Y^2({\log_{3}{5})}}=5^{\log_{2}{3}}$$, then Y equals to:
CAT 2020 Slot 1 - Question 52
A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
789
456
123
0.-
Clear All
CAT 2020 Slot 1 - Question 53
How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7?
789
456
123
0.-
Clear All
CAT 2020 Slot 1 - Question 54
The number of real-valued solutions of the equation $$2^{x}+2^{-x}=2-(x-2)^{2}$$ is:
CAT 2020 Slot 1 - Question 55
How many disticnt positive integer-valued solutions exist to the equation $$(x^{2}-7x+11)^{(x^{2}-13x+42)}=1$$ ?
CAT 2020 Slot 1 - Question 56
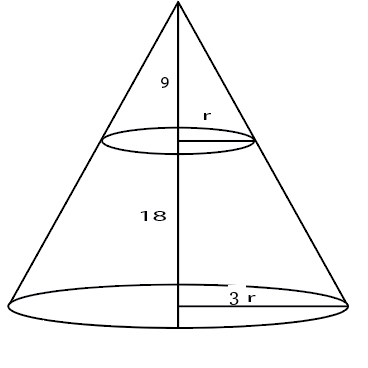
A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
CAT 2020 Slot 1 - Question 57
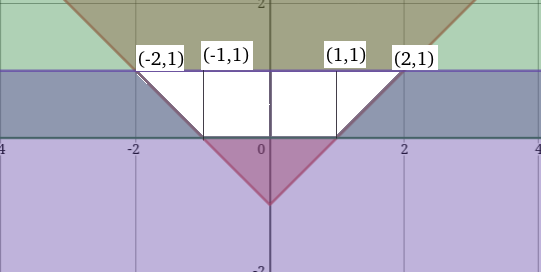
The area of the region satisfying the inequalities $$\mid x\mid-y\leq1,y\geq0$$ and $$y\leq1$$ is
789
456
123
0.-
Clear All
CAT 2020 Slot 1 - Question 58
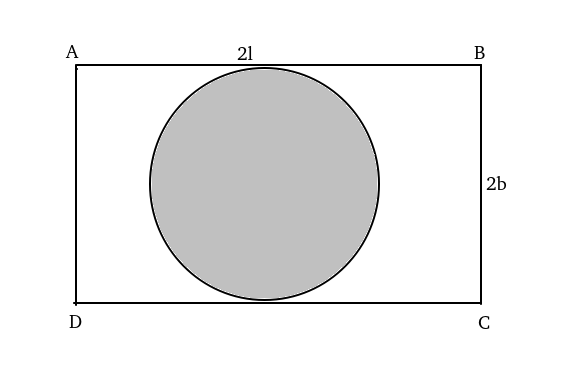
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
CAT 2020 Slot 1 - Question 59
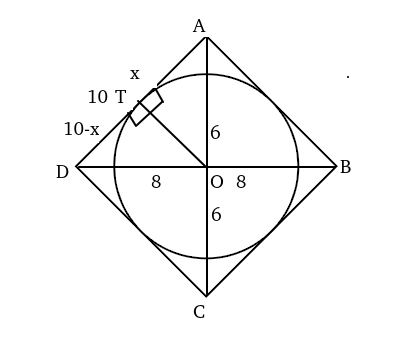
A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
CAT 2020 Slot 1 - Question 60
Among 100 students, $$x_1$$ have birthdays in January, $$X_2$$ have birthdays in February, and so on. If $$x_0=max(x_1,x_2,....,x_{12})$$, then the smallest possible value of $$x_0$$ is
Two Factor Authentication
Incase of any issue contact support@cracku.in