CAT 2018 Slot 2 Question Paper
For the following questions answer them individually
CAT 2018 Slot 2 - Question 71
The scores of Amal and Bimal in an examination are in the ratio 11 : 14. After an appeal, their scores increase by the same amount and their new scores are in the ratio 47 : 56. The ratio of Bimal’s new score to that of his original score is
CAT 2018 Slot 2 - Question 72
How many two-digit numbers, with a non-zero digit in the units place, are there which are more than thrice the number formed by interchanging the positions of its digits?
789
456
123
0.-
Clear All
CAT 2018 Slot 2 - Question 73
For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
789
456
123
0.-
Clear All
CAT 2018 Slot 2 - Question 74
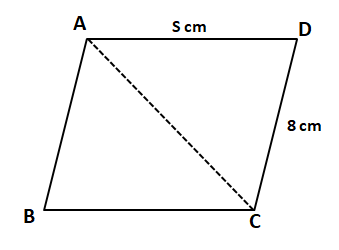
A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?
CAT 2018 Slot 2 - Question 75
A 20% ethanol solution is mixed with another ethanol solution, say, S of unknown concentration in the proportion 1:3 by volume. This mixture is then mixed with an equal volume of 20% ethanol solution. If the resultant mixture is a 31.25% ethanol solution, then the unknown concentration of S is
CAT 2018 Slot 2 - Question 76
In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match. There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches in senior level is 276. The number of matches a boy plays against a girl is
789
456
123
0.-
Clear All
CAT 2018 Slot 2 - Question 77
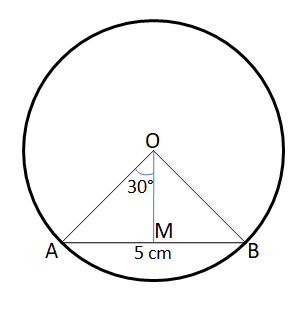
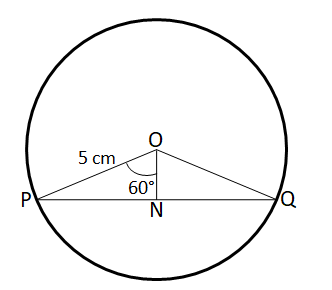
A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is
CAT 2018 Slot 2 - Question 78
Let $$\ a_{1},a_{2}...a_{52}\ $$ be positive integers such that $$\ a_{1}$$ < $$a_{2}$$ < ... < $$a_{52}\ $$. Suppose, their arithmetic mean is one less than arithmetic mean of $$a_{2}$$, $$a_{3}$$, ....$$a_{52}$$. If $$a_{52}$$= 100, then the largest possible value of $$a_{1}$$is
CAT 2018 Slot 2 - Question 79
The value of the sum 7 x 11 + 11 x 15 + 15 x 19 + ...+ 95 x 99 is
789
456
123
0.-
Clear All
CAT 2018 Slot 2 - Question 80
If N and x are positive integers such that $$N^{N}$$ = $$2^{160}\ and \ N{^2} + 2^{N}\ $$ is an integral multiple of $$\ 2^{x}$$, then the largest possible x is
789
456
123
0.-
Clear All
Two Factor Authentication
Incase of any issue contact support@cracku.in