A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is

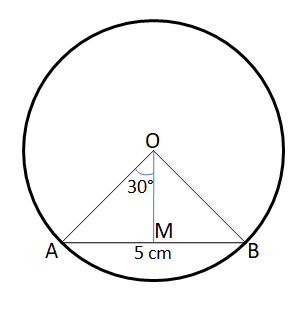
We are given that AB = 5 cm and $$\angle$$ AOB = 60°

Let us draw OM such that OM $$\perp$$ AB. 

In right angle triangle AMO,

$$sin 30° = \dfrac{AM}{AO}$$

$$\Rightarrow$$ AO = 2*AM = 2*2.5 = 5 cm. Therefore, we can say that the radius of the circle = 5 cm. 

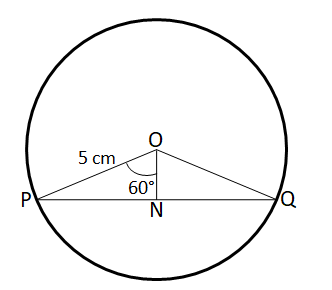
In right angle triangle PNO,

$$sin 60° = \dfrac{PN}{PO}$$

$$\Rightarrow$$ PN = $$\dfrac{\sqrt{3}}{2}$$*PO = $$\dfrac{5\sqrt{3}}{2}$$

Therefore, PQ = 2*PN = $$5\sqrt{3}$$ cm