Data Interpretation is one of the most important topics in the CAT LRDI Section. If you’re new to these questions, you can check out these CAT Data Interpretation Questions from the CAT previous year papers. In this article, we will look into some very important Data Interpretation questions PDF(with solutions) for CAT. You can also download these CAT Data Interpretation questions with detailed solutions, which also include important tricks to solve these questions.
Download Data Interpretation Questions for CAT
Enroll for CAT 2022 Online Course
Instructions
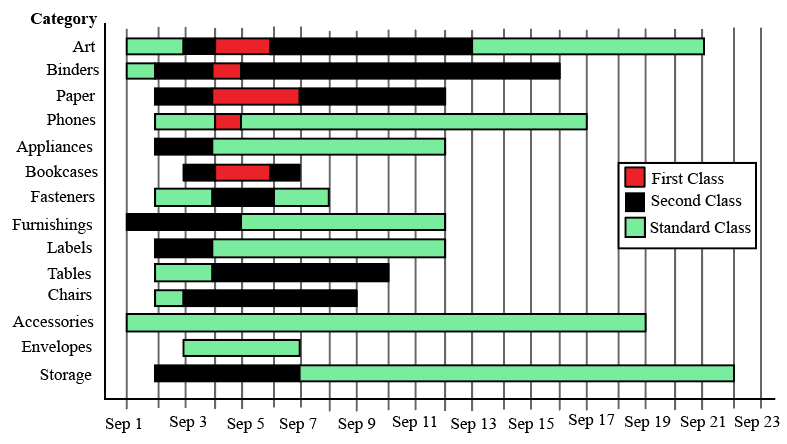
The different bars in the diagram above provide information about different orders in various categories (Art, Binders, ….) that were booked in the first two weeks of September of a store for one client. The colour and pattern of a bar denotes the ship mode (First Class / Second Class / Standard Class). The left end point of a bar indicates the booking day of the order, while the right end point indicates the dispatch day of the order. The difference between the dispatch day and the booking day (measured in terms of the number of days) is called the processing time of the order. For the same category, an order is considered for booking only after the previous order of the same category is dispatched. No two consecutive orders of the same category had identical ship mode during this period.
For example, there were only two orders in the furnishing category during this period. The first one was shipped in the Second Class. It was booked on Sep 1 and dispatched on Sep 5. The second order was shipped in the Standard class. It was booked on Sep 5 (although the order might have been placed before that) and dispatched on Sep 12. So the processing times were 4 and 7 days respectively for these orders.
Question 1:Â How many days between Sep 1 and Sep 14 (both inclusive) had no booking from this client considering all the above categories?
1)Â Answer:Â 6
Solution:
Accumulating all the data :
We get the following table :
Note a-b : represents the duration where a is the day when order is booked and b is the day when it is dispatched .
Now No booking days from the table are : September 8,9,10,11,12 and 14.
So a total of 6 days .
Question 2:Â What was the average processing time of all orders in the categories which had only one type of ship mode?
2)Â Answer:Â 11
Solution:
Accumulating all the data :
We get the following table :
Note a-b : represents the duration where a is the day when order is booked and b is the day when it is dispatched .
Now Envelopes and Accessories has only 1 ship mode i.e Standard class .
So therefore processing days for envelopes = 7-3 =4
and processing days for accessories = 19-1 =18
Therefore average =Â $\frac{\left(18+4\right)}{2}=11$
Question 3:Â The sequence of categories — Art, Binders, Paper and Phones — in decreasing order of average processing time of their orders in this period is:
a)Â Art, Binders, Paper, Phones
b)Â Phones, Art, Binders, Paper
c)Â Phones, Binders, Art, Paper
d)Â Paper, Binders, Art, Phones
3) Answer (B)
Solution:
Accumulating all the data :
We get the following table :
Note a-b : represents the duration where a is the day when order is booked and b is the day when it is dispatched .
Now taking average processing time per order for the above mentioned categories we get :
Art =$\frac{2+8+2+1+7}{5}\ \ =4$
Binders =$\frac{1+1+11+2}{4}\ \ =3.75$
Papers =Â $\frac{3+2+5}{3}\ \ =3.33$
Phones =$\frac{2+12+1}{3}\ \ =5$
So in decreasing order we get Phones , Art ,Binder , Paper.
Question 4:Â Approximately what percentage of orders had a processing time of one day during the period Sep 1 to Sep 22 (both dates inclusive)?
a)Â 22%
b)Â 16%
c)Â 20%
d)Â 25%
4) Answer (C)
Solution:
Accumulating all the data :
We get the following table :
Note a-b : represents the duration where a is the day when order is booked and b is the day when it is dispatched .
Now from the table we observe that the total number of orders are 35 and 7 orders have a processing time of 1 unit
The 7 orders are : Arts Standard class,Binders First class and standard class, Phones First class, Bookcases second class ( 2 orders)Â and Chairs standard class.
So the percentage = $\frac{7}{35}\times\ 100\ =\ 20$
Instructions
The figure above shows the schedule of four employees – Abani, Bahni, Danni, and Tinni – whom Dhoni supervised in 2020. Altogether there were five projects which started and concluded in 2020 in which they were involved. For each of these projects and for each employee, the starting day was at the beginning of a month and the concluding day was the end of a month, and these are indicated by the left and right end points of the corresponding horizontal bars. The number within each bar indicates the percentage of assigned work completed by the employee for that project, as assessed by Dhoni.
For each employee, his/her total project-month (in 2020) is the sum of the number of months (s)he worked across the five projects, while his/her annual completion index is the weightage average of the completion percentage assigned from the different projects, with the weights being the corresponding number of months (s)he worked in these projects. For each project, the total employee-month is the sum of the number of months four employees worked in this project, while its completion index is the weightage average of the completion percentage assigned for the employees who worked in this project, with the weights being the corresponding number of months they worked in this project.
Question 5:Â Which of the following statements is/are true?
I: The total project-month was the same for the four employees.
II: The total employee-month was the same for the five projects.
a)Â Only II
b)Â Both I and II
c)Â Neither I nor II
d)Â Only I
5) Answer (D)
Solution:
The total project month is the number of months Abani, Bahni, Danni, and Tinni individually worked for all the projects combined :
Abani – 2+2+5 = 9 months
Bahni – 2+4+3 = 9 months
Danni – 3+3+2+1 = 9 months
Tinni – 2+2+3+2 = 9 months.
The total employee month for all the five projects is the sum of the total employee-month is the sum of the number of months four employees worked in this project.
Project -1 = 2+2+2 = 6 months
Project -2 = 3+2 = 5 months
Project – 3 = 2+4+3 = 9 months.
Project – 4 = 5+2+3 = 10 months.
Project – 5 = 3+1+2 = 6 months.
Only statement 1 is true.
Question 6:Â Which employees did not work in multiple projects for any of the months in 2020?
a)Â Only Abani, Bahni and Danni
b)Â Only Abani and Bahni
c)Â All four of them
d)Â Only Tinni
6) Answer (A)
Solution:
Abani, Banni, and Danni did not work on multiple projects simultaneously in a month
Tinni was the only person who worked on multiple projects which are project 4 and project 5 in the month of september.
Question 7:Â The project duration, measured in terms of the number of months, is the time during which at least one employee worked in the project. Which of the following pairs of the projects had the same duration?
a)Â Project 1, Project 5
b)Â Project 4, Project 5
c)Â Project 3, Project 5
d)Â Project 3, Project 4
7) Answer (D)
Solution:
Considering the information provided :
For project 1 : 3 months.
Project – 2: 3 months.
Project – 3: 5 months.
Project – 4: 5 months.
Project – 5: 4 months.
Among the given options option D is true which is project 3, project 4.
Question 8:Â The list of employees in decreasing order of annual completion index is:
a)Â Danni, Tinni, Bahni, Abani
b)Â Bahni, Abani, Tinni, Danni
c)Â Danni, Tinni, Abani, Bahni
d)Â Tinni, Danni, Abani, Bahni
8) Answer (C)
Solution:
The annual completion index for different people is :
The weightage average of the completion percentage assigned from the different projects, with the weights being the corresponding number of months (s)he worked in these projects.
For Abani :
$\frac{\left(\left(100\cdot2\right)+\left(100\cdot2\right)+\left(80\cdot5\right)\right)}{2+2+5}=\ \frac{800}{9}$
For Bahni :
$\frac{\left(\left(100\cdot2\right)+\left(75\cdot4\right)+\left(90\cdot3\right)\right)}{2+3+4}=\ \frac{770}{9}$
For Danni :
$\frac{\left(\left(90\cdot3\right)+\left(100\cdot3\right)+\left(100\cdot2\right)+\left(100\cdot1\right)\right)}{2+3+2+1}=\ \frac{870}{9}$
For Tinni :
$\frac{\left(\left(80\cdot2\right)+\left(100\cdot2\right)+\left(100\cdot3\right)+\left(100\cdot2\right)\right)}{2+2+3+2}=\ \frac{860}{9}$
The descending order for the four people is :
Danni, Tinni, Abani, Bahni.
Instructions
DIRECTIONS for the following four questions:
A low-cost airline company connects ten India cities, A to J. The table below gives the distance between a pair of airports and the corresponding price charged by the company. Travel is permitted only from a departure airport to an arrival airport. The customers do not travel by a route where they have to stop at more than two intermediate airports.
<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI_6_3.png”/>
Question 9:Â What is the lowest possible fare, in rupees, from A to J?
a)Â 2275
b)Â 2850
c)Â 2890
d)Â 2930
e)Â 3340
9) Answer (A)
Solution:
From the table we can see that, the lowest price would be from A to H and H to J.
The cost of travel from A to H = Rs 1850
The cost of travel from H to J = Rs 425
Total cost = 1850 + 425 = Rs 2275.
Question 10:Â The company plans to introduce a direct flight between A and J. The market research results indicate that all its existing passengers travelling between A and J will use this direct flight if it is priced 5% below the minimum price that they pay at present. What should the company charge approximately, in rupees, for this direct flight?
a)Â 1991
b)Â 2161
c)Â 2707
d)Â 2745
e)Â 2783
10) Answer (B)
Solution:
From the table we can see that, the lowest price would be from A to H and H to J.
The cost of travel from A to H = Rs 1850
The cost of travel from H to JÂ = Rs 425
Total cost = 1850 + 425 = Rs 2275
Lowest price = Rs 2275
95% of 2275 = Rs 2161
Checkout: CAT Free Practice Questions and Videos
Question 11:Â If the airports C, D and H are closed down owing to security reasons, what would be the minimum price, in rupees, to be paid by a passenger travelling from A to J?
a)Â 2275
b)Â 2615
c)Â 2850
d)Â 2945
e)Â 3190
11) Answer (C)
Solution:
If the airports C, D and H are closed down  the minimum price to be paid by a passenger travelling from A to J would be by first travelling to F and then from F to J.
The cost of travel from A to FÂ = Rs 1700
The cost of travel from FÂ to JÂ = Rs 1150
Total cost = 1700 + 1150 = Rs 2850
Question 12:Â If the prices include a margin of 10% over the total cost that the company incurs, what is the minimum cost per kilometer that the company incurs in flying from A to J?
a)Â 0.77
b)Â 0.88
c)Â 0.99
d)Â 1.06
e)Â 1.08
12) Answer (B)
Solution:
The minimum cost from A to J we know is 2275.
Let the CP to company be C
Since 10% over actual CP is the total price i.e. $\text{CP}\times1.1 = 2275 \rightarrow CP = \frac{2275}{1.1}$
The total distance is 1950+1400=2350 Km.
Cost per Km = $\dfrac{\frac{2275}{1.1}}{2350}$ = Rs 0.88/Km
Question 13:Â If the prices include a margin of 15% over the total cost that the company incurs, which among the following is the distance to be covered in flying from A to J that minimizes the total cost of travel for the company?
a)Â 2170
b)Â 2180
c)Â 2315
d)Â 2350
e)Â 2390
13) Answer (D)
Solution:
Even if If the prices include a margin of 15% over the total cost that the company incurs, the total cost company incurs would be minimum for route AHJ i.e 2350 km. Hence option D.
Instructions
Simple Happiness index (SHI) of a country is computed on the basis of three, parameters: social support (S),freedom to life choices (F) and corruption perception (C). Each of these three parameters is measured on a scale of 0 to 8 (integers only). A country is then categorised based on the total score obtained by summing the scores of all the three parameters, as shown in the following table:
Following diagram depicts the frequency distribution of the scores in S, F and C of 10 countries – Amda, Benga, Calla, Delma, Eppa, Varsa, Wanna, Xanda,Yanga and Zooma:
Further, the following are known.
1. Amda and Calla jointly have the lowest total score, 7, with identical scores in all the three parameters.
2. Zooma has a total score of 17.
3. All the 3 countries, which are categorised as happy, have the highest score ln exactly one parameter.
Question 14:Â What is Amda’s score in F?
14)Â Answer:Â 1
Solution:
The frequency distribution is:
S:Â 3,3,3,4,4,4,5,5,6,7
F:Â 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
or
S: 3,3,3,4,4,4,5,5,6,7
F:Â 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
Given Amda and Cadella score is 7 each with identical in all parameters. So it can score either 3,1,3 in S,F,C respectively or 4,1,2 in S,F,C respectively. In both the cases, its score in F is 1.
Question 15:Â What is Zooma’s score in S?
15)Â Answer:Â 6
Solution:
The frequency distribution is:
S: 3,3,3,4,4,4,5,5,6,7
F: 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
or
S: 3,3,3,4,4,4,5,5,6,7
F:Â 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
Zooma(Z) has a total score of 17 (comes under happy category), and other 2Â countries, which are categorized as happy, have the highest score in exactly one parameter.
Suppose the other two countries are P and Q
Z have two possibilities for S, F, C : (6,7,4) & (6,5,6)
All the other cases are negated because “All the 3 countries, which are categorised as happy, have the highest score ln exactly one parameter.”
For Example : 7,7,3 is not possible because 7 being the highest score is there in two parameters.
So, it scored 6 in S in both the cases.
Checkout: CAT Free Practice Questions and Videos
Question 16:Â Benga and Delma, two countries categorized as happy, are tied with the same total score. What is the
maximum score they can have?
a)Â 14
b)Â 15
c)Â 16
d)Â 17
16) Answer (B)
Solution:
S:Â 3,3,3,4,4,4,5,5,6,7
F:Â 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
Benga and Delma, two countries categorized as happy, are tied with the same total score.
The best numbers remaining are 7,5,6 which adds upto 18, If Benga scores 18, then Delma can’t score 18.
Similarly both can’t score 17 and 16. Both can score 15 and their distribution will be:
Benga: 7,5,3
Delma: 4,5,6 or 5,4,6
Question 17:Â If Benga scores 16 and Delma scores 15, then what is the maximum number of countries with a score of 13?
a)Â 0
b)Â 1
c)Â 2
d)Â 3
17) Answer (B)
Solution:
S:Â 3,3,3,4,4,4,5,5,6,7
F:Â 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
Given that Benga scores 16, and Delma scores 15.
The possibility is Benga: 5,5,6 and Delma: 7,5,3
If Benga’s distribution is 7,3,6 then Delma can’t score 15.
Strike off those numbers.
S:Â 3,3,3,4,4,4,5,5,6,7
F:Â 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
We have to maximum number of countries with score 13. This score does not comes under the category of happy. So to score 13, the distribution can be 5,5,3. Hence, maximum 1 country is possible.
Instructions
The multi-layered pie-chart below shows the sales of LED television sets for a big retail electronics outlet during 2016 and 2017. The outer layer shows the monthly sales during this period, with each label showing the month followed by sales figure of that month. For some months, the sales figures are not given in the chart. The middle-layer shows quarterwise aggregate sales figures (in some cases, aggregate quarter-wise sales numbers are not given next to the quarter). The innermost layer shows annual sales. It is known that the sales figures during the three months of the second quarter (April, May, June) of 2016 form an arithmetic progression, as do the three monthly sales figures in the fourth quarter (October, November, December) of that year.
Question 18:Â What is the percentage increase in sales in December 2017 as compared to the sales in December 2016?
a)Â 38.46
b)Â 22.22
c)Â 28.57
d)Â 50.00
18) Answer (C)
Solution:
We have been given details about the quarterly sales figures. Also, we have been given details about the sales figures every month. Some of the data are missing and some additional conditions have been given in the question. Let us try to complete the pie chart as much as possible with the data available to us.
It is known that the sales figures during the three months of the second quarter (April, May, June) of 2016 form an arithmetic progression.
We know that the sales in April is 40.
Let the sales in May be 40+x and the sales in June be 40+2x.
We know that the total sales in Q2 is 150.
=> 40 + 40 + x + 40 + 2x = 150
3x = 30
x = 10
Therefore, sales in May 2016 = 40 + 10 = 50
Sales in June 2016 = 40 + 20 = 60
Similarly, it has been given that the sales in October, November, and December 2016 form an arithmetic progression.
Sales in October = 100
Sales in Q4 = 360
Let the sales in November be 100+y and the sales in December be 100+2y.
100 + 100 + y + 100 + 2y = 360
300 + 3y = 360
=> y = 20
Sales in November 2016 = 120 and Sales in December 2016 = 140
Sales in Q1 of 2016 = Sum of the sales in the months of January, February, and March 2016
= 80 + 60 + 100
= 240
Sales in Q3 of 2016 = Sum of the sales in the months of July, August, and September 2016
= 75 + 120 + 55
= 250
Sales in Q1 of 2017 = 120 + 100 + 160 = 380
Sales in Q2 of 2017 = 65 + 75 + 60 = 200
We know that sales in Q3 of 2017 = 220
Let the sales in August of 2017 be ‘a’.
60 + 70 + a = 220
=> a = 90
Sales in August 2017 = 90
We know that sales in Q4 of 2017 = 500
Let the sales in December of 2017 be ‘d’.
150 + 170 + d = 500
=> d = 180
Sales in December 2017 = 180
Sales in December 2016 = 140
Sales in December 2017 = 180
Percentage change = (180-140)/140 = 40/140 = 28.57%
Therefore, option C is the right answer.
Question 19:Â In which quarter of 2017 was the percentage increase in sales from the same quarter of 2016 the highest?
a)Â Q2
b)Â Q1
c)Â Q4
d)Â Q3
19) Answer (B)
Solution:
We have been given details about the quarterly sales figures. Also, we have been given details about the sales figures every month. Some of the data are missing and some additional conditions have been given in the question. Let us try to complete the pie chart as much as possible with the data available to us.
It is known that the sales figures during the three months of the second quarter (April, May, June) of 2016 form an arithmetic progression.
We know that the sales in April is 40.
Let the sales in May be 40+x and the sales in June be 40+2x.
We know that the total sales in Q2 is 150.
=> 40 + 40 + x + 40 + 2x = 150
3x = 30
x = 10
Therefore, sales in May 2016 = 40 + 10 = 50
Sales in June 2016 = 40 + 20 = 60
Similarly, it has been given that the sales in October, November, and December 2016 form an arithmetic progression.
Sales in October = 100
Sales in Q4 = 360
Let the sales in November be 100+y and the sales in December be 100+2y.
100 + 100 + y + 100 + 2y = 360
300 + 3y = 360
=> y = 20
Sales in November 2016 = 120 and Sales in December 2016 = 140
Sales in Q1 of 2016 = Sum of the sales in the months of January, February, and March 2016
= 80 + 60 + 100
= 240
Sales in Q3 of 2016 = Sum of the sales in the months of July, August, and September 2016
= 75 + 120 + 55
= 250
Sales in Q1 of 2017 = 120 + 100 + 160 = 380
Sales in Q2 of 2017 = 65 + 75 + 60 = 200
We know that sales in Q3 of 2017 = 220
Let the sales in August of 2017 be ‘a’.
60 + 70 + a = 220
=> a = 90
Sales in August 2017 = 90
We know that sales in Q4 of 2017 = 500
Let the sales in December of 2017 be ‘d’.
150 + 170 + d = 500
=> d = 180
Sales in December 2017 = 180
Among the given 4 options, we have to find the quarter in which the increase in sale from the previous quarter was the highest.
Q2:
Sales in 2017 = 200
Sales in 2016 = 150
Q1:
Sales in 2017 = 380
Sales in 2016 = 240
Q3:
Sales in 2017 = 220
Sales in 2016 = 250
Q4:
Sales in 2017 = 500
Sales in 2016 = 360
We can eliminate Q3 since the sales has decreased.
Growth in Q2 sales = 50/150 = 1/3 = 33.33%
Growth in Q1 sales = (380-240)/240 = 140/240 = 58.33%
Growth in Q4 sales = (500-360)/360 = 140/360
140/240 > 140/360
Therefore, Q1 has recorded the highest growth in sales and hence, option B is the right answer.
Question 20: During which quarter was the percentage decrease in sales from the previous quarter’s sales the highest?
a)Â Q2 of 2017
b)Â Q4 of 2017
c)Â Q2 of 2016
d)Â Q1 of 2017
20) Answer (A)
Solution:
We have been given details about the quarterly sales figures. Also, we have been given details about the sales figures every month. Some of the data are missing and some additional conditions have been given in the question. Let us try to complete the pie chart as much as possible with the data available to us.
It is known that the sales figures during the three months of the second quarter (April, May, June) of 2016 form an arithmetic progression.
We know that the sales in April is 40.
Let the sales in May be 40+x and the sales in June be 40+2x.
We know that the total sales in Q2 is 150.
=> 40 + 40 + x + 40 + 2x = 150
3x = 30
x = 10
Therefore, sales in May 2016 = 40 + 10 = 50
Sales in June 2016 = 40 + 20 = 60
Similarly, it has been given that the sales in October, November, and December 2016 form an arithmetic progression.
Sales in October = 100
Sales in Q4 = 360
Let the sales in November be 100+y and the sales in December be 100+2y.
100 + 100 + y + 100 + 2y = 360
300 + 3y = 360
=> y = 20
Sales in November 2016 = 120 and Sales in December 2016 = 140
Sales in Q1 of 2016 = Sum of the sales in the months of January, February, and March 2016
= 80 + 60 + 100
= 240
Sales in Q3 of 2016 = Sum of the sales in the months of July, August, and September 2016
= 75 + 120 + 55
= 250
Sales in Q1 of 2017 = 120 + 100 + 160 = 380
Sales in Q2 of 2017 = 65 + 75 + 60 = 200
We know that sales in Q3 of 2017 = 220
Let the sales in August of 2017 be ‘a’.
60 + 70 + a = 220
=> a = 90
Sales in August 2017 = 90
We know that sales in Q4 of 2017 = 500
Let the sales in December of 2017 be ‘d’.
150 + 170 + d = 500
=> d = 180
Sales in December 2017 = 180
Q2 of 2017:
Sales in Q2 of 2017 = 200
Sales in Q1 of 2017 = 380
% decrease = 180/380
Q4 of 2017:
We can eliminate this option since the sales has increased in Q4 of 2017 as compared to the previous quarter.
Q2 of 2016:
Sales in Q2 of 2016 = 150
Sales in Q1 of 2016 = 240
% decrease = 90/240
Q1 of 2017:
Sales in Q1 of 2017 has increased as compared to sales in the previous quarter. We can eliminate this option as well.
180/380 is very close to 50%. 90/240 is closer to 33.33%. Therefore, option A is the right answer.
Question 21: During which month was the percentage increase in sales from the previous month’s sales the highest?
a)Â March of 2017
b)Â October of 2017
c)Â March of 2016
d)Â October of 2016
21) Answer (B)
Solution:
We have been given details about the quarterly sales figures. Also, we have been given details about the sales figures every month. Some of the data are missing and some additional conditions have been given in the question. Let us try to complete the pie chart as much as possible with the data available to us.
It is known that the sales figures during the three months of the second quarter (April, May, June) of 2016 form an arithmetic progression.
We know that the sales in April is 40.
Let the sales in May be 40+x and the sales in June be 40+2x.
We know that the total sales in Q2 is 150.
=> 40 + 40 + x + 40 + 2x = 150
3x = 30
x = 10
Therefore, sales in May 2016 = 40 + 10 = 50
Sales in June 2016 = 40 + 20 = 60
Similarly, it has been given that the sales in October, November, and December 2016 form an arithmetic progression.
Sales in October = 100
Sales in Q4 = 360
Let the sales in November be 100+y and the sales in December be 100+2y.
100 + 100 + y + 100 + 2y = 360
300 + 3y = 360
=> y = 20
Sales in November 2016 = 120 and Sales in December 2016 = 140
Sales in Q1 of 2016 = Sum of the sales in the months of January, February, and March 2016
= 80 + 60 + 100
= 240
Sales in Q3 of 2016 = Sum of the sales in the months of July, August, and September 2016
= 75 + 120 + 55
= 250
Sales in Q1 of 2017 = 120 + 100 + 160 = 380
Sales in Q2 of 2017 = 65 + 75 + 60 = 200
We know that sales in Q3 of 2017 = 220
Let the sales in August of 2017 be ‘a’.
60 + 70 + a = 220
=> a = 90
Sales in August 2017 = 90
We know that sales in Q4 of 2017 = 500
Let the sales in December of 2017 be ‘d’.
150 + 170 + d = 500
=> d = 180
Sales in December 2017 = 180
March of 2017:
Sales in March of 2017 = 160
Sales in February of 2017 = 100
% increase = 60/100 = 60%
October of 2017:
Sales in October of 2017 = 150
Sales in September of 2017 = 70
As we can see, the sales has increased by more than 100%.
March of 2016:
Sales in March of 2016 = 100
Sales in February of 2016 = 60
% increase in sales is less than 100%.
October of 2016:
Sales in October of 2016 = 100
Sales in September of 2016 = 55
% increase is less than 100%
As we can see, the percentage increase in sale as compared to the previous month was highest in October of 2017 among the given options. Therefore, option B is the right answer
DILR Videos | Preparation Videos for CAT DILR
-
Also, check out CAT Previous year Questions with detailed solutions here.
- Try these 3 Cracku Free CAT Mocks, which come with detailed solutions and with video explanations.
