Question 8
In a circle with centre O, ABCD isa cyclic quadrilateral and AC is the diameter. Chords AB and CD are produced to meet at E. If $$\angle CAE = 34^\circ$$ and $$\angle E = 30^\circ$$, then $$\angle CBD$$ is equal to:
Solution
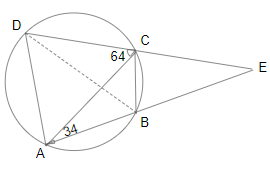
By the exterior angle property,
$$\angle DCA$$ = 30 + 34 = 64
$$\angle DAC$$ = 180 - 90 - 64 = 26$$\degree$$
$$\angle DAC = \angle CBD$$
$$\angle CBD = 26\degree$$
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Remainders QuestionsCAT Mensuration QuestionsCAT Time And Work QuestionsCAT Probability, Combinatorics QuestionsCAT Percentages Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Quant Based LR QuestionsCAT Table with Missing values QuestionsCAT Scheduling QuestionsCAT Data Interpretation Basics QuestionsCAT DI Miscellaneous Questions
