Question 41
The height of a cone is 45 cm. It is cut at a height of 15 cm from its base by a plane parallel to its base. If the volume of the smaller cone is 2310 $$cm^3$$, then what is the volume (in $$cm^3$$) of the original cone?
Solution
We have :
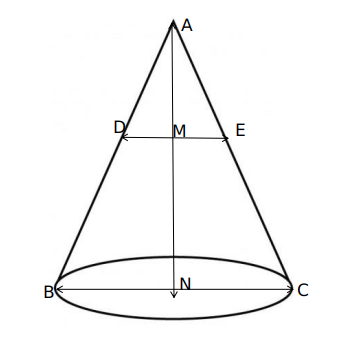
AM =15 ;AN=45
Now radius of smaller cone = rÂ
Now we know that Triangles AME and ANC are similar
so we can say
AM:AN = ME:NC
So we can say NC=3r.
Now $$\frac{1}{3}\pi\ \times\ r^2\times\ 15\ =2310$$ Â (1)
Now Volume of larger cone = $$\frac{1}{3}\pi\ \times\ 9r^2\times\ 45\ =V$$ Â (2)
Dividing (2) and (1)
we get 27:1 =V/2310
We get V = 62,370
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
