In the given figure, 3 semicircles are drawn on three sides of triangle ABC. AB = 21 cm, BC = 28 cm and AC = 35 cm. What is the area (in $$cm^2$$) of the shaded part?

We have :

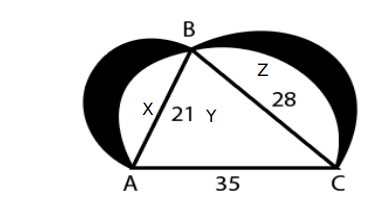
Here X,Y and Z denote the regions

Now triangle with sides 21,28 and 35 forms a right triangle 
Now area of triangle ABC = $$\frac{1}{2}\times\ 21\times\ 28$$
=294 square units
Now Area of X + Shaded 1 (Region on AB) = Area of semicircle with radius 10.5
we get X +S1 = $$\frac{22}{7}\times\ 10.5\times\ \frac{10.5}{2}$$ =693/4      (1)
Now similarly Z+S2 = $$\frac{22}{7}\times\ 14\times\ \frac{14}{2}$$ = 308      (2)
Now X+Z = $$\frac{22}{7}\times\ 35\times\ \frac{35}{2}-294$$    (3)
Now Adding 1 and 2 and subtracting 3 from their addition
we will get area of shaded region
Now solving we get
Area of Shaded region = 294