In the given figure, $$PQR$$ is an equilateral triangle with side as 12 $$cm$$. $$S$$ and $$T$$ are the mid points of the sides $$PQ$$ and $$PR$$ respectively. What is the area (in $$cm^2$$) of the shaded region?

We have :

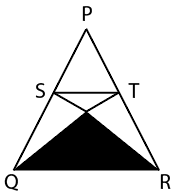
Now QT and SR intersect at O and they are medians 
so O will be centroid 
Now QO:TO =2:1 and RO:SO=2:1
Now are of triangle = $$\frac{\sqrt{\ 3}}{4}\times\ 12\times\ 12=36\sqrt{\ 3}$$
Now we know that Triangle PST is similar to triangle PQR
so area of PST: area of PQR = (PS:PQ)^2=1/4
so we get area of PST = $$9\sqrt{\ 3}$$
and area of STRQ =$$27\sqrt{\ 3}$$
Now let area of STO = A
so we get area of QOA = 4A ( similar triangle )
Now since QO:TO =2:1
so area of QOS = 2A
similarly area of ROT =2A
Adding all we get 9A =$$27\sqrt{\ 3}$$
A=$$3\sqrt{\ 3}$$
Therefore 4A =$$12\sqrt{\ 3}$$