In a square of side 2 meters, isosceles triangles of equal area are cut from the corners to form a regular octagon. Find the perimeter and area of the rectangular octagon.

Let us assume that 'a' is the length of the side of equal sides of the isosceles triangle. 

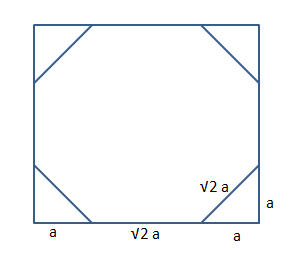
We can see that $$a+\sqrt{2}*a+a=2$$

$$\Rightarrow$$ a = $$\dfrac{2}{2+\sqrt{2}}$$

Therefore, the perimeter of the regular octagon = $$8*a*\sqrt{2}$$

$$\Rightarrow$$ $$\dfrac{8\sqrt{2}*2}{2+\sqrt{2}}$$

$$\Rightarrow$$ $$\dfrac{16}{1+\sqrt{2}}$$ ... (1)

Area of regular octagon = $$2x^2(1+\sqrt{2})$$ where 'x' is the length of each side. 

Here, x = $$a\sqrt{2}$$ = $$\dfrac{2\sqrt{2}}{2+\sqrt{2}}$$ = $$\dfrac{2}{1+\sqrt{2}}$$

Therefore, area of the regular octagon = $$2*(\dfrac{2}{1+\sqrt{2}})^2(1+\sqrt{2})$$ = $$\dfrac{8}{1+\sqrt{2}}$$ =$$\dfrac{8}{1+\sqrt{2}}*\dfrac{1+\sqrt{2}}{1+\sqrt{2}}$$ = $$\dfrac{8*(1+\sqrt{2})}{3+2\sqrt{2}}$$

Hence, we can say that none of the given answer is correct.