Simple Happiness index (SHI) of a country is computed on the basis of three, parameters: social support (S),freedom to life choices (F) and corruption perception (C). Each of these three parameters is measured on a scale of 0 to 8 (integers only). A country is then categorised based on the total score obtained by summing the scores of all the three parameters, as shown in the following table:
Following diagram depicts the frequency distribution of the scores in S, F and C of 10 countries - Amda, Benga, Calla, Delma, Eppa, Varsa, Wanna, Xanda,Yanga and Zooma:
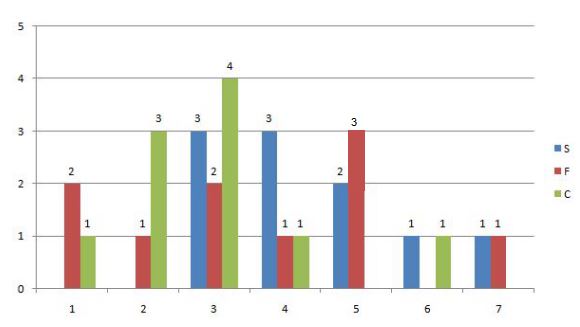
Further, the following are known.
1. Amda and Calla jointly have the lowest total score, 7, with identical scores in all the three parameters.
2. Zooma has a total score of 17.
3. All the 3 countries, which are categorised as happy, have the highest score ln exactly one parameter.
If Benga scores 16 and Delma scores 15, then what is the maximum number of countries with a score of 13?
S: 3,3,3,4,4,4,5,5,6,7
F: 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
Given that Benga scores 16, and Delma scores 15.
The possibility is Benga: 5,5,6 and Delma: 7,5,3
If Benga's distribution is 7,3,6 then Delma can't score 15.
Strike off those numbers.
S: 3,3,3,4,4,4,5,5,6,7
F: 1,1,2,3,3,4,5,5,5,7
C: 1,2,2,2,3,3,3,3,4,6
We have to maximum number of countries with score 13. This score does not comes under the category of happy. So to score 13, the distribution can be 5,5,3. Hence, maximum 1 country is possible.
Video Solution
