Sign in
Please select an account to continue using cracku.in
↓ →
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
If the numbers of students enrolled in K and L are in the ratio 19:22, then what is the number of students enrolled in L?
Let 'x' be the number of students enrolled in all three sports. Then the number of students enrolled only in L = 2x
It is given that there are a total of 17 students enrolled in G. Also, ten students enrolled in G are also enrolled in at least one more sport. Hence, the number of students enrolled in only G = 17 - 10 = 7

The number of students enrolled only in G is one less than the number of students enrolled only in L. Hence, the number of students enrolled only in L = 7+1
$$\Rightarrow$$ 2x = 8
$$\Rightarrow$$ x = 4
Let us assume that 'y' students are enrolled in K and L but not G. Then, the number of students enrolled only in K = y + 4
Let us assume that 'z' be the the number of students enrolled in G and K but not L. Then, the number of students enrolled G and L bot not K = 10 - 4 - z = 6 - z
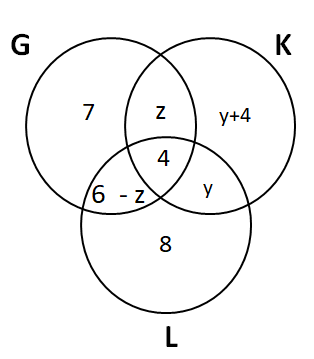
It is given that a total of 39 students in the sports.
7 + z + 4 + 6 - z + 8 + y + y + 4 = 39
$$\Rightarrow$$ y = 5
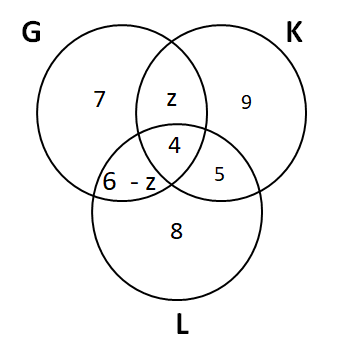
Number of students enrolled in G = 17
Number of students enrolled in K = 9 + 4 + 5 + z = 18 + z
Number of students enrolled in L = 6 - z + 4 + 5 + 8 = 23 - z
It is given that the maximum student enrollment is in L.
$$\Rightarrow$$ 23 - z > 18 + z
$$\Rightarrow$$ 2z < 5
$$\Rightarrow$$ z < 2.5
Therefore, we can say that z can take three values = {0, 1, 2}
It is given that the numbers of students enrolled in K and L are in the ratio 19:22.
$$\dfrac{18+z}{23-z} = \dfrac{19}{22}$$
z = 1 which is a possible solution as well.
In this case the number of students enrolled in L = 23 - z = 23 - 1 = 22. Hence, option C is the correct answer.

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation