XAT 2020 Question Paper
For the following questions answer them individually
XAT 2020 - Question 61
A rectangular field is 40 meters long and 30 meters wide. Draw diagonals on this field and then draw circles of radius 1.25 meters, with centers only on the diagonals. Each circle must fall completely within the field. Any two circles can touch each other but should not overlap. What is the maximum number of such circles that can be drawn in the field?
XAT 2020 - Question 62
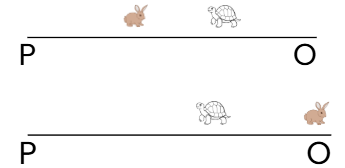
A hare and a tortoise run between points O and P located exactly 6 km from each other on a straight line. They start together at O, go straight to P and then return to O along the same line. They run at constant speeds of 12 km/hr and 1 km/hr respectively. Since the tortoise is slower than the hare, the hare shuttles between O and P until the tortoise goes once to P and returns to O. During the run, how many times are the hare and the tortoise separated by an exact distance of 1 km from each other?
XAT 2020 - Question 63
Consider the four variables A, B, C and D and a function Z of these variables, $$Z = 15A^2 - 3B^4 + C + 0.5D$$ It is given that A, B, C and D must be non-negative integers and thatall of the following relationships must hold:
i) $$2A + B \leq 2$$
ii) $$4A + 2B + C \leq 12$$
iii) $$3A + 4B + D \leq 15$$
If Z needs to be maximised, then what value must D take?
XAT 2020 - Question 64
XYZ is an equilateral triangle, inscribed in a circle. P is a point on the arc YZ such that X and P are on opposite sides of the chord YZ. Which of the following MUST always be true?
XAT 2020 - Question 65
X, Y and Z start a web-based venture together. X invests Rs. 2.5 lakhs, Y invests Rs. 3.5 lakhs, and Z invests Rs. 4 lakhs. In the first year, the venture makes a profit of Rs. 2 lakhs. A part of the profit is shared between Y and Z in the ratio of 2:3, and the remaining profit is divided among X, Y and Z in the ratio of their initial investments. The amount that Z receives is four times the amount that X receives. How much amount does Y receive?
XAT 2020 - Question 66
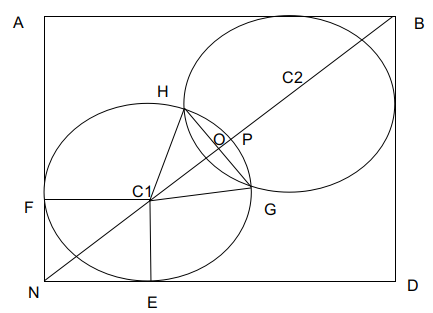
Mohanlal, a prosperous farmer, has a square land of side 2 km. For the current season, he decides to have some fun. He marks two distinct points on one of the diagonals of the land. Using these points as centers, he constructs two circles. Each of these circles falls completely within the land, and touches at least two sides of the land. To his surprise, the radii of both the circles are exactly equal to $$\frac{2}{3}$$ km. Mohanlal plants potatoes on the overlapping portion of these circles. Calculate the area on which Mohanlal planted potatoes (in sq. km).
Read the information given below and answer the 2 associated questions.
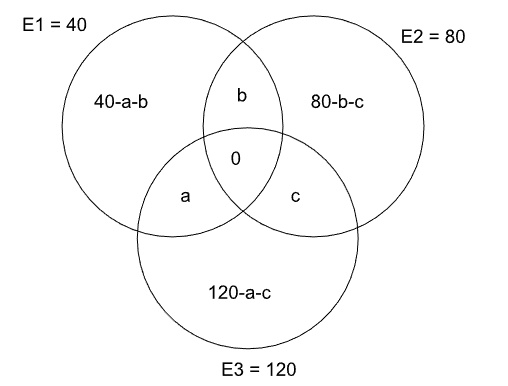
190 students have to choose at least one elective and at most two electives from a list of three electives: E1, E2 and E3. It is found that the number of students choosing E1 is half the number of students choosing E2, and one third the number of students choosing E3.
Moreover, the number of students choosing two electives is 50.
XAT 2020 - Question 67
Which of the following CANNOT be obtained from the given information?
XAT 2020 - Question 68
In addition to the given information, which of the following information is NECESSARY and SUFFICIENT to compute the number of students choosing only E1, only E2 and only E3?
For the following questions answer them individually
XAT 2020 - Question 69
Ashok has a bag containing 40 cards, numbered with the integers from 1 to 40. No two cards are numbered with the same integer. Likewise, his sister Shilpa has another bag containing only five cards that are numbered with the integers from 1 to 5, with no integer repeating. Their mother, Latha, randomly draws one card each from Ashok’s and Shilpa’s bags and notes down their respective numbers. If Latha divides the number obtained from Ashok’s bag by the number obtained from Shilpa’s, what is the probability that the remainder will not be greater than 2?
XAT 2020 - Question 70
X, Y, and Z are three software experts, who work on upgrading the software in a number of identical systems. X takes a day off after every 3 days of work, Y takes a day off after every 4 days of work and Z takes a day off after every 5 days of work.
Starting afresh after a common day off,
i) X and Y working together can complete one new upgrade job in 6 days
ii) Z and X working together can complete two new upgrade jobs in 8 days
iii) Y and Z working together can complete three new upgrade jobs in 12 days.
If X, Y and Z together start afresh on a new upgrade job (after a common day off), exactly how many days will be required to complete this job?
Two Factor Authentication
Incase of any issue contact support@cracku.in


.webp)