Mohanlal, a prosperous farmer, has a square land of side 2 km. For the current season, he decides to have some fun. He marks two distinct points on one of the diagonals of the land. Using these points as centers, he constructs two circles. Each of these circles falls completely within the land, and touches at least two sides of the land. To his surprise, the radii of both the circles are exactly equal to $$\frac{2}{3}$$ km. Mohanlal plants potatoes on the overlapping portion of these circles. Calculate the area on which Mohanlal planted potatoes (in sq. km).
Solution
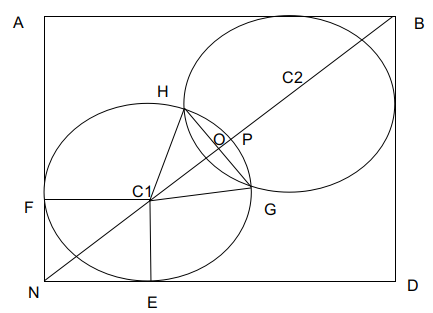
The two circles are symmetric about the diagonal.
NC1=$$\frac{2\sqrt{\ 2}}{3}$$ = $$\sqrt{\ \left(\frac{2}{3}\right)^{^2}+\left(\frac{2}{3}\right)^2}=\ \frac{\left(2\sqrt{\ 2}\right)}{3}$$
The lengths FC1, EC1 are the radius of the circle which is 2km/3.
The length C1P is the radius of the circle.
Because of symmetry C1O = C2O and C1N = C2B.
2*(C1N+ C1O) = $$2\sqrt{\ 2}$$ the length of the diagonal of the square.
C1N+C1O = $$\sqrt{\ 2}$$
C1O = $$\sqrt{\ 2}-\frac{2\sqrt{\ 2}}{3}=\ \frac{\sqrt{\ 2}}{3}$$
OP = $$\frac{\left(2-\sqrt{\ 2}\right)}{3}$$
The diagonal perpendicularly bisects the line GH. Hence C1OH is 90 degrees.$$C1H^2\ =\ C1O^2+OH^2$$
OH = $$\frac{\sqrt{\ 2}}{3}$$. Similarly OG = $$\frac{\sqrt{\ 2}}{3}$$
HC1, C1G both are equal to $$\frac{2}{3}$$ each. H1G is $$\frac{2\sqrt{\ 2}}{3}$$. HC1G is a raight angled traingle with angle HC1G is 90 degrees.
Area of the region required is 2*(Area of segment OGH)
.'. Area of required region=$$2\left(\frac{90}{360}\cdot\frac{4\pi\ }{9}-\frac{1}{2}\cdot\frac{2\sqrt{\ 2}}{3}\cdot\frac{\sqrt{\ 2}}{3}\right)$$=$$\frac{2(\pi - 2)}{9}$$
Video Solution

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
