Given, a+b+c=50 and a+b+c+x+y+z=190 => x+y+z=140.

Also, let E1=k => E2=2k and E3=3k ---------------1

Also, E1 = (x+a+0+b) , E2 = (y+b+0+c) , E3 = (z+a+0+c) ----------------2

From 1, E1+E2+E3 = 6k and from 2, E1+E2+E3 = (x+y+z)+2(a+b+c) = 140 + 2*50 = 240

=> 6k = 240

=> k = 40

Thus our venn diagram will look like this - 

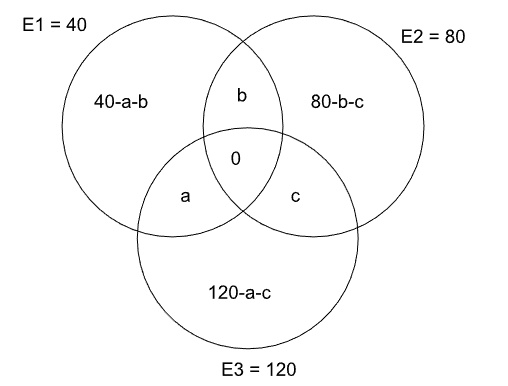
Option A: If the number of students choosing only E2 and the number of students choosing both E2 and E3 are given, then we know the value of (80-b-c) [ which will provide us with the value of (b+c) ], and the value of c. Since we know the value of c, we can get the value of b. And as the values of b and c are known, the value of a can also be known. Thus, we can find all the values. 

Option B: Knowing the number of students choosing both E1 and E2, the number of students choosing both E2 and E3, and the number of students choosing both E3 and E1 is SUFFICIENT as we will get the values of a, b, and c. However, this information is not NECESSARY when calculating the number of students who choose only E1, E2, and E3 because we can calculate that with fewer conditions (like in option A).

Option C: Number of students choosing only E1, and number of students choosing both E2 and E3. Thus, we know the value of (40-a-b), which will provide us with the value of (a+b), and we know the value of c. However, the individual values of a and b cannot be known. Thus, we won't be able to find the number of students who choose only E1, only E2, and only E3.

Option D: Some extra information about a, b, and c is necessary. Thus, this option is incorrect. 

Option E: Number of students choosing both E1 and E2. This will give us the value of b, and since we know the value of (a+b+c), thus we can find the value of a+c. But the individual values of a and c  cannot be known. Thus, this is also incorrect.