IPM Indore 2025 Question Paper
For the following questions answer them individually
IPM Indore 2025 - Question 21
A natural number n lies between 100 and 400, and the sum of its digits is 10. The probability that n is divisible by 4, is
IPM Indore 2025 - Question 22
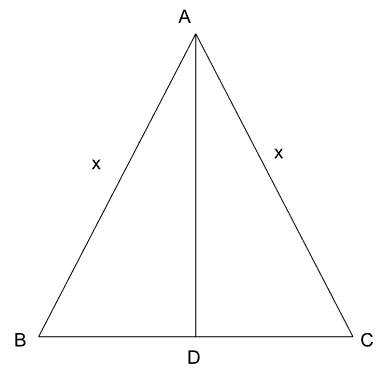
In triangle ABC, AB = AC = x, $$\angle ABC = \theta$$ and the circumradius is equal to y. Then $$\frac{x}{y}$$ equals
IPM Indore 2025 - Question 23
If $$8x^2 - 2kx + k = 0$$ is a quadratic equation in x, such that one of its roots is p times the other, and p, k are positive real numbers, then k equals
IPM Indore 2025 - Question 24
Let A(1, 3) and B(5, 1) be two points. If a line with slope m intersects AB at anangle of $$45^\circ$$, then the possible values of m are
IPM Indore 2025 - Question 25
Let P(x) be a quadratic polynomial such that $$\begin{vmatrix}P(0) & P(1)\\P(0) & P(2)\end{vmatrix} = 0$$ Let P(0) = 2 and P(1) + P(2) + P(3) = 14. Then P(4) equals
IPM Indore 2025 - Question 26
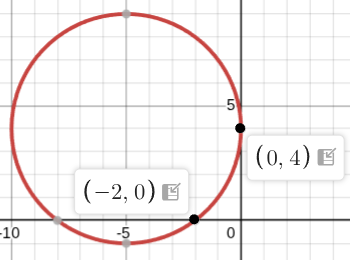
A circle touches the y-axis at (0, 4) and passes through the point (-2, 0). Then theradius of the circle is
IPM Indore 2025 - Question 27
Consider a triangle with side lengths 4 meters, 6 meters, and 9 meters. A dog runs around the triangle in such a way that the shortest distance of the dog from the triangle is exactly 1 meter. The total distance covered (in meters) by the dog in one round is
IPM Indore 2025 - Question 28
Anindita invests a total of 1 lakh rupees distributed across three schemes, A, B and C, for a period of two years. These schemes offer an interest rate of 10%, 8% and 12% per annum, respectively, each compounded annually. If the initial investment amount in scheme A is 30000 rupees and the total interest earned from all three schemes during the first year is 10600 rupees, then the total interest earned, in rupees, from all three schemes for the second year is
IPM Indore 2025 - Question 29
Let $$f(x) = a^2x^2 + 2bx + c$$ where, $$a \neq 0, b, c$$ are real numbers and x is a real variable then
IPM Indore 2025 - Question 30
The area of the triangle, formed by the straight lines y = 0, 12x - 5y = 0, and $$3x + 4y = 7$$ is