In triangle ABC, AB = AC = x, $$\angle ABC = \theta$$ and the circumradius is equal to y. Then $$\frac{x}{y}$$ equals

In triangle ABC, AB = AC = x, therefore $$\angle ABC=\angle ACB=\theta\ $$, since angles opposite to equal sides are equal. Let AD be the perpendicular to BC.

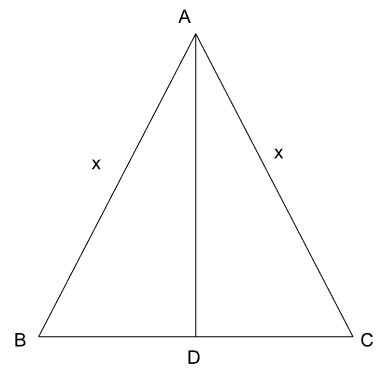
$$\cos\theta=\dfrac{base}{hypoteneuse}=\dfrac{BD}{AB}=\dfrac{BD}{x}$$ => $$BD=x\cos\theta$$

$$\cos\theta=\dfrac{base}{hypoteneuse}=\dfrac{CD}{AB}=\dfrac{CD}{x}$$ => $$CD=x\cos\theta$$

=> $$BC=BD+DC=2x\cos\theta$$

$$\sin\theta=\dfrac{perpendicular}{hypoteneuse}=\dfrac{AD}{AB}=\dfrac{AD}{x}$$ => $$AD=x\sin\theta$$

It is given that the circumradius of the triangle is y.

We also know that => $$Area\ of\ \triangle=\dfrac{abc}{4R}$$, where R is the circumradius, and a, b, and c are the sides of the triangle.

=> $$\dfrac{1}{2}\times2x\cos\theta\times x\sin\theta\ =\dfrac{x\times x\times2x\cos\theta\ }{4y}$$

=> $$\dfrac{1}{2}\times2x^2\cos\theta\sin\theta\ =\dfrac{2x^3\cos\theta\ }{4y}$$

=> $$\dfrac{1}{2}\times\sin\theta\ =\dfrac{x\ }{4y}$$

=> $$\dfrac{x\ }{y}=2\sin\theta\ $$