The area of the triangle, formed by the straight lines y = 0, 12x - 5y = 0, and $$3x + 4y = 7$$ is
Solution
We are given 3 lines : y = 0, $$12x - 5y = 0$$ , and $$3x + 4y = 7$$ . The triangle formed by these three lines will have its vertices at the points of intersection of the lines with each other. These points can be found by solving the equations simultaneously.
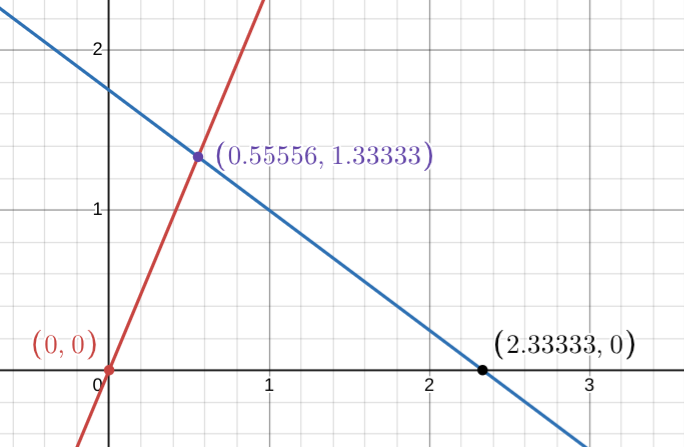
The lines y=0 and 12x-5y=0 intersect at x=0 ie (0,0)
The lines y=0 and 3x+4y=0 intersect at x= $$\frac{7}{3}$$ ie $$\left(\frac{7}{3},0\right)$$
And the intersection point of the lines 12x-5y=0 and 3x+4y=0 is found to be $$\left(\frac{5}{9},\frac{4}{3}\right)$$
So the area of the triangle formed by these 3 vertices is given by the formula $$\triangle\ =\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|$$
Taking (0,0), $$\left(\frac{7}{3},0\right)$$, and $$\left(\frac{5}{9},\frac{4}{3}\right)$$ as (x1,y1),(x2,y2) and (x3,y3) we have ,
$$\triangle\ =\frac{1}{2}\left|0\left(0-\frac{4}{3}\right)+\frac{7}{3}\left(\frac{4}{3}-0\right)+\frac{5}{9}\left(0-0\right)\right|$$
or, $$\triangle\ =\frac{1}{2}\left|0+\frac{28}{9}+0\right|=\frac{14}{9}$$ sq units.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

