Area of a regular octagon inscribed in a circle of radius 1 unit is:
Solution
The figure below represents a regular octagon ABCDEFGH inscribed in a circle with center at O and radius 1 unit.
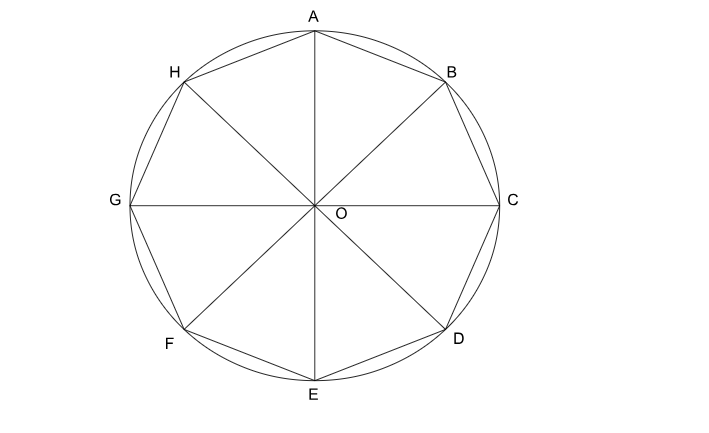
Since the octagon is a regular octagon, on drawing diagonals AE, BF, CG, and DH, all of them will pass through the center. We can therefore divide the octagon into 8 congruent isosceles triangles.
Hence, OA=OBV=OC=OD=OE=OF=OG=OH=1 unit(since all of them are radii of the same circle)
And, AB=BC=CD=DE=EF=FG=GH=HA ( since all of them are sides of the same regular octagon)
So we can say that $$\triangle AOB,\ \triangle BOC,\ \triangle COD,\ \triangle DOE,\ \triangle EOF,\ \triangle FOG,\ \triangle GOH\ and\ \triangle HOA\ $$ are all congruent triangles, which would mean that all the angles at the center are also equal.
So, $$\angle\ AOB=\frac{360}{8}=45^{\circ\ }$$
Hence, area of$$\triangle AOB=\frac{1}{2}\times\ AO\times\ BO\times\ \sin\ \left(\angle\ AOB\right)=\frac{1}{2}\times\ 1\times\ 1\times\ \sin\ 45=\frac{1}{2\sqrt{\ 2}}\ sq\ units$$
As the octagon is divided into 8 congruent triangles, so the area of the octagon is $$\frac{1}{2\sqrt{\ 2}}\times\ 8=2\sqrt{\ 2}\ sq\ units$$
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

