Question 29

Let $$f(x) = a^2x^2 + 2bx + c$$ where, $$a \neq 0, b, c$$ are real numbers and x is a real variable then

Solution
Share

$$f(x) = a^2x^2 + 2bx + c$$

$$a^2$$ is a positive number. This means the coefficient of $$x^2$$ is a positive number. Whenever the coefficient of $$x^2$$ is positive, the graph will look something like this - 

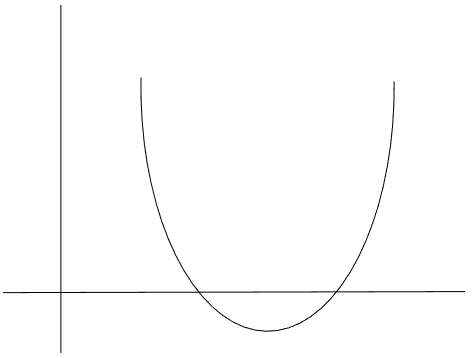
image

Thus, we can see that this graph will have a definite minimum, but no definite maximum value. 

View More Questions From Temporary

Create a FREE account and get:

  • Download Maths Shortcuts PDF
  • Get 300+ previous papers with solutions PDF
  • 500+ Online Tests for Free