IPM Indore 2025 Question Paper
For the following questions answer them individually
IPM Indore 2025 - Question 11
Monica, who is 18 years old, is one-third the age of her father. The age at which she will be half the age of her father is ____
789
456
123
0.-
Clear All
IPM Indore 2025 - Question 12
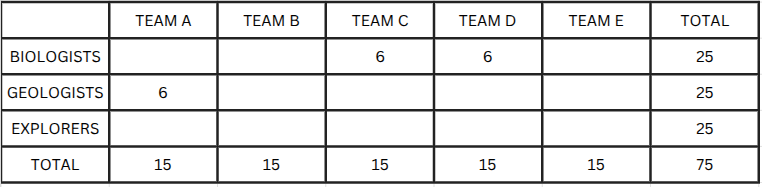
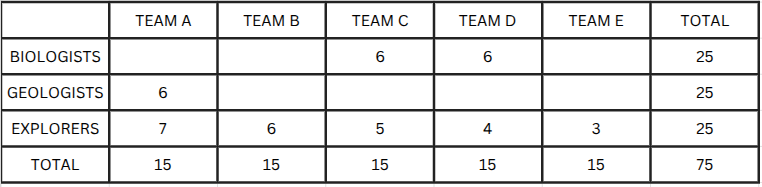
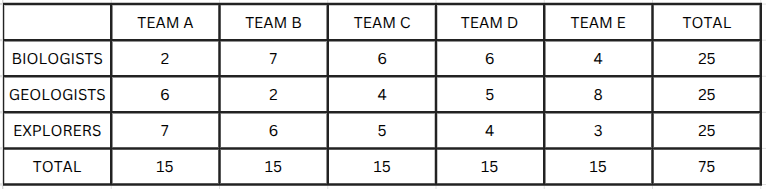
Five teams - A, B, C, D, and E - each consisting of 15 members, are going on expeditions to five different locations.Each team includes members from three different skill sets: biologists, geologists, and explorers. However, the number of members from each skill set varies by team, and each member has only one speciality. The total number of biologists, geologists, and explorers is equal.
The following additional information is available
- Every team has at least 2 members from each skill set.
- Teams C and D have 6 biologists each, and Team A has 6 geologists.
- Every team except A has more biologists than explorers.
- The number of explorers in each team is distinct and decreases in the order A, B, C, D, and E.
The median number of biologists across 5 teams is______
789
456
123
0.-
Clear All
IPM Indore 2025 - Question 13
If m and n are two positive integers such that 7m + 11n = 200, then the minimum possible value of m + n is
789
456
123
0.-
Clear All
IPM Indore 2025 - Question 14
The number of factors of $$3^5 \times 5^8 \times 7^2$$ that are perfect squares is
789
456
123
0.-
Clear All
IPM Indore 2025 - Question 15
If the polynomial $$ax^2 + bx + 5$$ leaves a remainder 3 when divided by $$x - 1$$, and a remainder 2 when divided by $$x + 1$$, then $$2b - 4a$$ equals
789
456
123
0.-
Clear All
IPM Indore 2025 - Question 16
Given that $$1 + \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2} + ...... = \dfrac{\pi^2}{6}$$, the value of $$1 + \dfrac{1}{3^2} + \dfrac{1}{5^2} + \dfrac{1}{7^2} + ......$$ is
IPM Indore 2025 - Question 17
If $$y = a + b \log_e x$$, which of the following is true?
IPM Indore 2025 - Question 18
If $$a_1, a_2, ......., a_8$$ are the roots of the equation $$x^8 + x^7 + ..... + x + 1 = 0$$, them the value of $$a^{2025}_1 + a^{2025}_2 + .... + a^{2025}_8$$ is
IPM Indore 2025 - Question 19
Suppose a, b and c are three real numbers such that Max(a, b, c) + Min(a, b, c) = 15, and Median(a, b, c) - Mean(a, b, c) = 2. Then the median of a, b and c is
IPM Indore 2025 - Question 20
If $$\log_{25}\left[5 \log_3 (1 + \log_3(1 + 2 \log_2 x))\right] = \frac{1}{2}$$ then x is: