IPM Indore 2025 Question Paper
For the following questions answer them individually
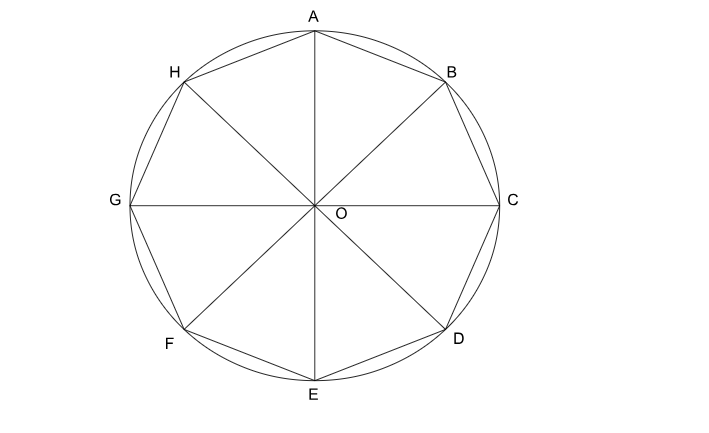
IPM Indore 2025 - Question 31
Area of a regular octagon inscribed in a circle of radius 1 unit is:
IPM Indore 2025 - Question 32
Two swimmers, Ankit and Bipul, start swimming from opposite ends of a swimming pool at the same time. Ankit can cover the length of the pool once in 10 minutes. Bipul can cover the length of the pool once in 15 minutes. They swim back and forth for 80 minutes without stopping. The number of times they meet each other is-
IPM Indore 2025 - Question 33
The sum of the first 5 terms of a geometric progression is the same as the sum of the first 7 terms of the same progression. If the sum of the first 9 terms is 24, then the 4th term of the progression is
IPM Indore 2025 - Question 34
The set of all values of x satisfying the inequality $$\log_{\left(x+\frac{1}{x}\right)}\left[\log_2\left(\frac{x-1}{x+2}\right)\right]>0$$ is
IPM Indore 2025 - Question 35
Let $$S_1 = \left\{100, 105, 110, 115, ...\right\}$$ and $$S_2 = \left\{100, 95, 90, 85, ...\right\}$$ be two series in arithmetic progression. If $$a_k$$ and $$b_k$$ are the $$k^{th}$$ terms of
$$S_1$$ and $$S_2$$, respectively, then $$\sum_{k=1}^{20}a_k b_k$$ equals ____________.
IPM Indore 2025 - Question 36
A and B take part in a rifle shooting match. The probability of A hitting the target is 0.4, while the probability of B hitting the target is 0.6. If A has the first shot, post which both strike alternately, then the probability that A hits the target before B hits it is
IPM Indore 2025 - Question 37
Which of the following numbers is divisible by $$3^{10} + 2$$
IPM Indore 2025 - Question 38
Let A and B be two finite sets such that $$n(A - B), n(A \cap B), n(B - A)$$ are in an arithmetic progression. Here n(X) denotes the number of elements in a finite set X. If $$n(A \cup B) = 18$$, then $$n(A) + n(B)$$ is __________
IPM Indore 2025 - Question 39
The number of integers greater than 5000 and divisible by 5 that can be formed withthe digits 1, 3, 5, 7, 8, 9 where no digit is repeated is
IPM Indore 2025 - Question 40
The remainder when $$11^{1011} + 1011^{11}$$ is divided by 9 is