CAT 2025 Slot 1
For the following questions answer them individually
CAT 2025 Slot 1 - Question 47
A value of $$c$$ for which the minimum value of $$f(x)=x^{2}-4cx+8c$$ is greater than the maximum value of $$g(x)=-x^{2}+3cx-2c$$, is
CAT 2025 Slot 1 - Question 48
Shruti travels a distance of 224 km in four parts for a total travel time of 3 hours. Her speeds in these four parts follow an arithmetic progression, and the corresponding time taken to cover these four parts follow another arithmetic progression. If she travels at a speed of 960 meters per minute for 30 minutes to cover the first part, then the distance, in meters, she travels in the fourth part is
CAT 2025 Slot 1 - Question 49
In a 3-digit number N, the digits are non-zero and distinct such that none of the digits is a perfect square, and only one of the digits is a prime number. Then, the number of factors of the minimum possible value of N is
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 50
Let $$3\leq x\leq6$$ and $$\left[x^{2}\right] =\left[x\right]^{2}$$ , where $$[x]$$ is the greatest integer not exceeding $$x$$ . If set $$S$$ represents all feasible values of $$x$$, then a possible subset of $$S$$ is
CAT 2025 Slot 1 - Question 51
Stocks A, B and C are priced at rupees 120, 90 and 150 per share, respectively. A trader holds a portfolio consisting of 10 shares of stock A, and 20 shares of stocks B and C put together. If the total value of her portfolio is rupees 3300, then the number of shares of stock B that she holds, is
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 52
For any natural number k , let $$a_{k}=3^{k}$$. The smallest natural number m for which $$\left\{(a_{1})^{1}\times(a_{2})^{2}\times...\times(a_{20})^{20}\right\}<\left\{a_{21}\times a_{22}\times...\times a_{20+m}\right\}$$, is
CAT 2025 Slot 1 - Question 53
The number of distinct integers $$n$$ for which $$\log_{\frac{1}{4}}({n^{2}-7n+11})>0$$,is
CAT 2025 Slot 1 - Question 54
The number of distinct pairs of integers (x, y) satisfying the inequalities $$x>y\geq3 $$ and $$x+y<14$$ is
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 55
At a certain simple rate of interest, a given sum amounts to Rs 13920 in 3 years, and to Rs 18960 in 6 years and 6 months. If the same given sum had been invested for 2 years at the same rate as before but with interest compounded every 6 months, then the total interest earned, in rupees, would have been nearest to
CAT 2025 Slot 1 - Question 56
A container holds 200 litres of a solution of acid and water, having 30% acid by volume. Atul replaces 20% of this solution with water, then replaces 10% of the resulting solution with acid, and finally replaces 15% of the solution thus obtained, with water. The percentage of acid by volume in the final solution obtained after these three replacements, is nearest to
CAT 2025 Slot 1 - Question 57
In a class, there were more than 10 boys and a certain number of girls. After 40% of the girls and 60% of the boys left the class, the remaining number of girls was 8 more than the remaining number of boys. Then, the minimum possible number of students initially in the class was
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 58
A cafeteria offers 5 types of sandwiches. Moreover, for each type of sandwich, a customer can choose one of 4 breads and opt for either small or large sized sandwich. Optionally, the customer may also add up to 2 out of 6 available sauces. The number of different ways in which an order can be placed for a sandwich, is
CAT 2025 Slot 1 - Question 59
In the set of consecutive odd numbers $$\left\{1,3,5,...,57\right\}$$, there is a number $$k$$ such that the sum of all the elements less than $$k$$ is equal to the sum of all the elements greater than $$k$$ . Then, $$k$$ equals
CAT 2025 Slot 1 - Question 60
Arun, Varun and Tarun, if working alone, can complete a task in 24, 21, and 15 days, respectively. They charge Rs 2160, Rs 2400, and Rs 2160 per day, respectively, even if they are employed for a partial day. On any given day, any of the workers may or may not be employed to work. If the task needs to be completed in 10 days or less, then the minimum possible amount, in rupees, required to be paid for the entire task is
CAT 2025 Slot 1 - Question 61
Kamala divided her investment of Rs 100000 between stocks, bonds, and gold. Her investment in bonds was 25% of her investment in gold. With annual returns of 10%, 6%, 8% on stocks, bonds, and gold, respectively, she gained a total amount of Rs 8200 in one year. The amount, in rupees, that she gained from the bonds, was
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 62
If $$a-6b+6c=4$$ and $$6a+3b-3c=50$$, where a, b and c are real numbers, the value of $$2a+3b-3c$$ is
CAT 2025 Slot 1 - Question 63
The (x, y) coordinates of vertices P, Q and R of a parallelogram PQRS are (-3, -2), (1, -5) and (9, 1), respectively. If the diagonal SQ intersects the x-axis at (a, 0) , then the value of a is
CAT 2025 Slot 1 - Question 64
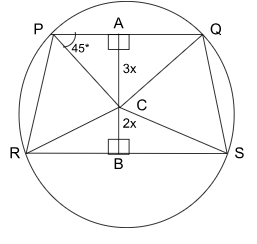
In a circle with center C and radius $$6\sqrt{2}$$ cm, PQ and SR are two parallel chords separated by one of the diameters. If $$\angle PQC=45^{0}$$, and the ratio of the perpendicular distance of $$PQ$$ and $$SR$$ from $$C$$ is $$3:2$$, then the area, in sq. cm, of the quadrilateral $$PQRS$$ is
CAT 2025 Slot 1 - Question 65
The ratio of the number of students in the morning shift and afternoon shift of a school was 13 : 9. After 21 students moved from the morning shift to the afternoon shift, this ratio became 19 : 14. Next, some new students joined the morning and afternoon shifts in the ratio 3 : 8 and then the ratio of the number of students in the morning shift and the afternoon shift became 5 : 4. The number of new students who joined is
CAT 2025 Slot 1 - Question 66
If the length of a side of a rhombus is 36 cm and the area of the rhombus is 396 sq. cm, then the absolute value of the difference between the lengths, in cm, of the diagonals of the rhombus is
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 67
The number of non-negative integer values of k for which the quadratic equation $$x^{2}-5x+k=0$$ has only integer roots, is
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 68
A shopkeeper offers a discount of 22% on the marked price of each chair, and gives 13 chairs to a customer for the discounted price of 12 chairs to earn a profit of 26% on the transaction. If the cost price of each chair is Rs 100, then the marked price, in rupees, of each chair is
789
456
123
0.-
Clear All