Sign in
Please select an account to continue using cracku.in
↓ →
The number of distinct pairs of integers (x, y) satisfying the inequalities $$x>y\geq3 $$ and $$x+y<14$$ is
Correct Answer: 16
It is given, $$x>y\geq3 $$ and $$x+y<14$$
Now for $$y=3$$, the values of $$x$$ can be 4,5,6,7,8,9,10 (7 cases)
Then for $$y=4$$, the values of $$x$$ can be 5,6,7,8,9 (5 cases)
Then for $$y=5$$, the values of $$x$$ can be 6,7,8 (3 cases)
Then for $$y=6$$, the values of $$x$$ will be 7 (1 case)
So, total number of cases =1+3+5+7=16 cases
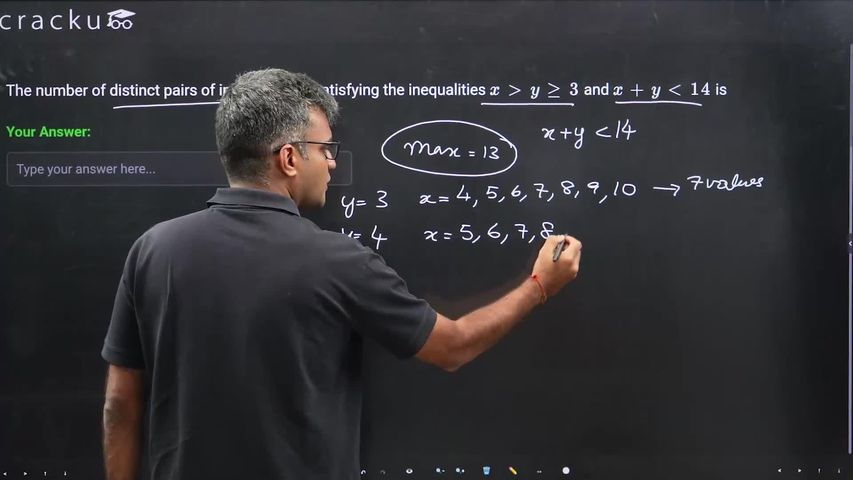
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation